Methodology Report #18:
Updates to the Medical Expenditure Panel Survey Insurance Component List Sample Design, 2004
John P. Sommers, PhD, Agency for Healthcare Research and Quality.
Table of Contents
Abstract
The Medical Expenditure Panel Survey (MEPS)
Background
Original List Sample Design
New Conditions and Information That Allow Updating the Sample Design
Allocation to States: Private Sector
Allocation within States: Private Sector
Changes in Restrictions on Maximum Sample Size per Firm
Government Sample Improvements
Summary
References
Appendix A. Private Sector Allocations and Response per State
Appendix B. Percent of Universe and Sample per Stratum: Private Sector
Appendix C. Methods for Reduction of Expected Sample for Private Sector Firms
Abstract
This report describes changes to the sample design for the Insurance Component
of the Medical Expenditure Panel Survey. The paper provides the background of
the original sample design and the conditions that now exist that allow for change
in this design. The report then describes the new strata and sample allocation
scheme for the private sector portion of the sample and how these changes were
developed, the changes made in a method used to restrict sample for private
sector employers to contain the burden for large employers, and the changes made
in the allocation of the survey’s government sample.
The estimates in this report are based on the most recent data available at the time
the report was written. However, selected elements of MEPS data may be revised
on the basis of additional analyses, which could result in slightly different
estimates from those shown here. Please check the MEPS Web site for the most
current file releases.
Center for Financing, Access, and Cost Trends
Agency for Healthcare Research and Quality
540 Gaither Road
Rockville, MD 20850
www.meps.ahrq.gov
The Medical Expenditure Panel Survey (MEPS)
Background
The Medical Expenditure Panel Survey (MEPS) is conducted
to provide nationally representative estimates of health care use,
expenditures, sources of payment, and insurance coverage for the U.S.
civilian noninstitutionalized population. MEPS is cosponsored by the Agency for Healthcare Research and
Quality (AHRQ), formerly the Agency for Health Care Policy and Research, and the
National Center for Health Statistics (NCHS).
MEPS comprises three component surveys: the Household
Component (HC), the Medical Provider Component (MPC), and the Insurance
Component (IC). The HC is the core survey, and it forms the basis for the MPC sample
and part of the IC sample. Together these surveys yield comprehensive data that
provide national estimates of the level and distribution of health care use and
expenditures, support health services research, and can be used to assess health care policy
implications.
MEPS is the third in a series of national probability
surveys conducted by AHRQ on the financing and use of medical care in the United States.
The National Medical Care Expenditure Survey (NMCES) was conducted in 1977, the
National Medical Expenditure Survey (NMES) in 1987. Beginning in 1996,
MEPS continues this series with design enhancements and efficiencies that provide a
more current data resource to capture the changing dynamics of the health care
delivery and insurance system.
The design efficiencies incorporated into MEPS are in
accordance with the Department of Health and Human Services (DHHS) Survey Integration
Plan of June 1995, which focused on consolidating DHHS surveys, achieving cost
efficiencies, reducing respondent burden, and enhancing analytical capacities.
To accommodate these goals, new MEPS design features include linkage with the
National Health Interview Survey (NHIS), from which the sample for the MEPS-HC is drawn,
and enhanced longitudinal data collection for core survey components. The MEPS-HC
augments NHIS by selecting a sample of NHIS respondents, collecting additional data
on their health care expenditures, and linking these data with additional
information collected from the respondents’ medical providers, employers, and insurance
providers.
Household Component
The MEPS-HC, a nationally representative survey of the
U.S. civilian noninstitutionalized population, collects medical
expenditure data at both the person and household levels. The HC
collects detailed data on demographic characteristics, health
conditions, health status, use of medical care services, charges and
payments, access to care, satisfaction with care, health insurance
coverage, income, and employment.
The HC uses an overlapping panel design in which data
are collected through a preliminary contact followed by a series of five
rounds of interviews over a two and a half year period. Using
computer-assisted personal interviewing (CAPI) technology, data on
medical expenditures and use for two calendar years are collected from
each household. This series of data collection rounds is launched each
subsequent year on a new sample of households to provide overlapping
panels of survey data and, when combined with other ongoing panels, will
provide continuous and current estimates of health care expenditures.
The sampling frame for the MEPS-HC is drawn from
respondents to NHIS, conducted by NCHS. NHIS provides a nationally
representative sample of the U.S. civilian noninstitutionalized
population, with oversampling of Hispanics and blacks.
Medical Provider Component
The MEPS-MPC supplements and validates information on
medical care events reported in the MEPS-HC by contacting medical
providers and pharmacies identified by household respondents. The MPC
sample includes all hospitals, hospital physicians, home health
agencies, and pharmacies reported in the HC. Also included in the MPC
are all office-based physicians:
-
Providing care for HC respondents receiving Medicaid.
-
Associated with a 75 percent sample of households receiving care through
an HMO (health maintenance organization) or managed care plan.
- Associated with a 25 percent sample of the remaining households. Data
are collected on medical and financial characteristics of medical and
pharmacy events reported by HC respondents, including:
- Diagnoses coded according to ICD-9 (9th Revision, International
Classification of Diseases) and DSMIV (Fourth Edition, Diagnostic and
Statistical Manual of Mental Disorders).
- Physician procedure codes classified by CPT-4 (Current Procedural
Terminology, Version 4).
- Inpatient stay codes classified by DRG (diagnosis related group).
- Prescriptions coded by national drug code (NDC), medication names,
strength, and quantity dispensed.
- Charges, payments, and the reasons for any difference between charges
and payments.
The MPC is conducted through telephone interviews and
mailed survey materials.
Insurance Component
The MEPS-IC collects data on health insurance plans
obtained through private and public sector employers. Data obtained in
the IC include the number and types of private insurance plans offered,
benefits associated with these plans, premiums, contributions by
employers and employees, and employer characteristics.
Establishments participating in the MEPS-IC are selected
through three sampling frames:
-
A list of employers or other insurance providers identified by MEPS-HC
respondents who report having private health insurance at the Round 1
interview.
-
A Bureau of the Census list frame of private-sector business establishments.
-
The Census of Governments from the Bureau of the Census.
To provide an integrated picture of health insurance,
data collected from the first sampling frame (employers and other
insurance providers) are linked back to data provided by the MEPS-HC
respondents. Data from the other three sampling frames are collected to
provide annual national and State estimates of the supply of private
health insurance available to American workers and to evaluate policy
issues pertaining to health insurance. Since 2000, the Bureau of
Economic Analysis has used national estimates of employer contributions
to group health insurance from the MEPS-IC in the computation of Gross
Domestic Product (GDP).
The MEPS-IC is an annual panel survey. Data are
collected from the selected organizations through a prescreening
telephone interview, a mailed questionnaire, and a telephone follow-up
for nonrespondents.
Survey Management
MEPS data are collected under the authority of the
Public Health Service Act. They are edited and published in accordance
with the confidentiality provisions of this act and the Privacy Act.
NCHS provides consultation and technical assistance.
As soon as data collection and editing are completed,
the MEPS survey data are released to the public in staged releases of
summary reports and microdata files. Summary reports are released as
printed documents and electronic files. Microdata files are released on
CD-ROM and/or as electronic files.
Printed documents and CD-ROMs are available through the AHRQ Publications
Clearinghouse. Write or call:
AHRQ Publications Clearinghouse
Attn: (publication number)
P.O. Box 8547 Silver Spring, MD 20907
800-358-9295
703-437-2078 (callers outside the United States only)
888-586-6340 (toll-free TDD service; hearing impaired only)
To order online, send an e-mail to: ahrqpubs@ahrq.gov.
Be sure to specify the AHRQ number of the document or CD-ROM you are
requesting. Selected electronic files are available through the Internet
on the MEPS Web site:
http://www.meps.ahrq.gov/
For more information, visit the MEPS Web site or e-mail mepspd@ahrq.gov.
Return to Table of Contents
Background
The Insurance Component of the Medical Expenditure Panel Survey (MEPS-IC) is an
annual national survey of business establishments (locations) and governments
sponsored by the Agency for Healthcare Research and Quality (AHRQ) and conducted
by the United States Census Bureau. The survey is designed to collect information on
employer-sponsored health insurance, such as whether insurance is offered and if so,
enrollments, premiums, employee contributions, and plan characteristics. Information
about the establishment or government, such as size and workforce characteristics, are
also collected to allow for modeling of results and estimation by different business or
government characteristics.
The MEPS-IC has two major purposes. The first is to collect information from
employers of household respondents to the MEPS Household Component (HC), a
household survey collecting information on health expenditures, use, insurance and
demographics of the noninstitutionalized population of the United States. This sample of
employers of the household respondents is known as the household sample (Cohen,
1996). These data are primarily used for modeling and are not collected annually.
Instead, the data are collected on a periodic basis. The second purpose of the survey is to
produce national- and state-level estimates of enrollments, premiums, and contributions
for a variety of categories, such as industry, firm size, and average payroll per employee.
This requires a random sample of business locations and governments, which for the
MEPS-IC is referred to as the list sample, because it is selected from lists maintained by
the Census Bureau. The original list sample, designed for the first MEPS-IC used for
collection of data for the year 1996 (years in this document will always refer to the year
of the data, not year of collection; collection of data crosses years), supported estimates
for the 40 largest states and the nation as a whole. However, in subsequent years, sample
sizes for the 20 smallest states were changed annually so that, although there were
published estimates for only 40 states in a given year, all 50 states and the District of
Columbia would have state-level estimates at least once every four years (MEPS
Insurance Component: Technical Notes and Survey Documentation).
Return to Table of Contents
Original List Sample Design
The original list sample design and allocation (Sommers, 1999) considered governments
and private sectors together in order to yield allocations that produced estimates with a
desired level of error at the state and national level for the entire set of employers, both
public and private sectors. This basic design, which was used with little change through
the 2002 survey, will be called the old, original, or current design within this document.
The updated design, which will be completely in place for the 2004 survey, will be
called the new design. After the original allocation took place, the sample was then
allocated within each state between the public and private sectors based upon each
sector’s proportion of total state employment. Within each sector, these allocations were
further allocated to individual strata. This design allowed for sufficient sample in the
largest states to support national and state estimates, while smaller states below a certain
size had minimum sample sizes assigned. These minimum sample sizes were generally
much larger than the sample otherwise required to support reliable national estimates.
However, the minimum sample sizes were required to support estimates for the
individual states.
Within each state, strata were formed based upon employment sizes, and sequential
sample selection methods were used to select the final samples. Because the public and
private sector lists of employers were maintained on two different lists, sampling for
public and private sectors was done separately once allocations were determined.
A unique feature of the MEPS-IC list sample is a restriction on the expected numbers of
establishments in the sample for a private sector firm. (A firm is an entity that controls
one or more business establishments or locations; for instance, General Motors is a firm
and an individual General Motors plant location is an establishment.) The reason for this
restriction was to limit the amount of collection burden on an individual firm, since most
firms require collection of information for all their establishments at a central location.
Because the MEPS-IC required collection of both the household and list samples of
establishments and the sample of establishments in the household sample was
predetermined, the restriction on firm size took place only on the list sample and was
very strict. This restriction significantly raises the design effect of the list sample
estimates. (Sommers, 1999 and Kish, 1965)
Return to Table of Contents
New Conditions and Information
That Allow Updating the Sample Design
Considerable knowledge has been gained since the 1996 MEPS-IC that can be used to
improve the sample design. During the same time period, operational conditions of the
survey have changed. These changes in operational climate also allow implementation of
methods that can improve the sample design. Following are the key new factors that
support improvement in the sample design of the survey:
-
Estimates of variance components have been made for a variety of important
variables. These estimates can be used to design new strata and test new sample
design proposals.
-
Extensive modeling has been done to gain knowledge of what ancillary information
is available for sampling units and best predicts survey outcomes, such as premiums
and enrollment rates. Such information can be used to develop better strata
boundaries.
-
The decision was made to suspend annual collection of the household sample.
-
Estimates of the private sector are required for states, not combined estimates of the
set of both private and public sector employees within the state.
Combinations of these items have motivated the following changes to the sample design:
-
The first two have allowed for the development of a new stratification and allocation
sample scheme for the survey.
-
The third and fourth items have allowed budget for extra sample to provide for
minimum samples for each state for the private sector alone rather than the
combination of public and private employers that was originally done, thus allowing
estimates for all states for the private sector alone.
-
The third item allowed changes in the restrictions for the maximum sample allowed
per firm. Because there is no longer an annual household sample, this allows
restrictions on the list sample to be loosened without affecting the overall burden on
individual firms.
-
The last item allowed development of a new government sample, totally independent
of any private sector design or allocation. There is no requirement for an over
sample of governments for smaller states.
The following sections discuss specific changes in the MEPS-IC sample design that will
result in an updated design by the year 2004. Included are descriptions of the changes,
how they were developed and the improvements in sampling errors that are expected as a
result of these changes.
Return to Table of Contents
Allocation to States: Private Sector
Allocation of private sector sample to states for the new design was done in a manner
similar to the allocation of total sample, government and private sector, for previous
surveys. First, the proportions of national payroll, employment, and number of
establishments were calculated for each state. For each state, these proportions were
averaged to give an average proportion across the three items. Using these average
proportions, 17,000 responding sample units were allocated proportionally to the states.
Any state with fewer than 560 units then had its allocation increased to 560 units. (Note
that in the samples prior to 2003, each state was allocated a responding sample of 600,
but this included governments. This new allocation is for the private sector only and thus
has a smaller minimum sample size than the old allocation. [Sommers, 1999] )
This initial sample allocation could not be afforded under the IC budget. To reduce
costs, the expected responding sample size for the smallest 11 states was reduced to 520.
This new allocation should give national results at least comparable to the current
sample if no other changes were made. For instance, the relative standard error for
estimates of the percentage of establishments that offer health insurance and the average
single premium would both be about 0.5 percent. The slight reduction in sample for the
smallest states would still allow the survey to meet this goal, since the larger sample in
these states has little effect on national estimates due to the very small portion of the
nation that these states represent.
Assuming the same variance structure within each state, the overall sampling of states in
this manner, with the resulting unequal weighting, creates a 20 percent increase in
standard errors for national estimates compared to a proportional allocation with equal
weights. Note that for the current sample (Sommers, 1999), where only 40 states had a
minimum sample size, there was only a 10 percent increase in standard errors in national
estimates due to the over sampling. However, the overall sample size was smaller. This
increase in sample size offsets the extra inefficiency caused by the increase in over
sampling of small states. With the extra sample, if no other changes were made to the
sample design except for the change in allocations to the states, the errors for national
estimates would be very comparable for both allocations.
The new allocations to states are presented in Appendix A.
Return to Table of Contents
Allocation within States: Private Sector
In order to reduce sampling error in IC estimates, new sampling strata were developed.
The original strata boundaries were developed by Westat as part of the work done on the
1993 National Employer Health Insurance Survey, a precursor to the IC. These strata
were based upon firm and establishment employment sizes (Marker, 1996). While
employment sizes correlate well with such important variables as whether an
establishment offers health insurance, the percentage of employees enrolled, and the
average premiums and contributions towards health insurance made by employers and
employees, over the years information that has been gathered has shown several other
independent descriptive variables also correlated with these outcome variables. Among
these variables are state, age of firm, industry, and average payroll of an establishment.
AHRQ decided that these variables also should be considered in production of IC strata
along with the important employment size variables.
The old stratification of the IC sample was done by simply crossing categories of firm
size and categories of establishment size to create 14 strata. However, due to the many
cells that would be created by crossing the categories of six different variables, another
method was needed to consider all the new variables in creating strata. Such a method
was required to limit the number of strata used. The method chosen was to use the set of
variables to create models that would predict the probability that an establishment would
offer health insurance and the expected percentage of employees at the establishment
that would enroll in insurance if offered. It was assumed that because the models were
based upon a large number of variables, each of which correlated with the key variables,
that the predicted values would correlate better with the final results than just the
employment size classes alone.
To test this hypotheses, three years of data were used, 1998–2000. Using 1999 data,
logistic regressions were run, the first to model the probability that an establishment had
health insurance and the second to model, for those with health insurance, the
probability that an employee would enroll. The models were used to predict values for
the entire frame for the 2000 survey year. Using the “cum square root f rule” (Cochran,
1977), the 2000 frame was broken into six strata based upon the establishment’s
probability of offering insurance.
After this was done, the three strata that contained establishments with the highest
probabilities of offering health insurance were broken into substrata using the “cum
square root f rule” applied to the expected number of enrollees in health insurance. The
stratum that contained the establishments with highest probability of offering health
insurance was broken into six substrata, the stratum that contained establishments with
the second most likely chances of offering health insurance was broken into three
substrata, and the stratum that contained establishments with the third highest
probability of offering health insurance was broken into two substrata. The reason for
the decreasing number of substrata was that as the probability of offering heath
insurance decreases, the range of sizes of establishments in the strata based upon this
probability decreases. Thus, the three strata with establishments that have the least likely
chance of offering health insurance, consist of only small establishments that do not
require substratification for the size of the potential enrollment. On the other hand, the
expected number of enrollees varies considerably within the stratum with establishments
with a high probability of offering health insurance. Breaking this stratum into substrata
assures that the variance across the total enrollment within each substratum will be
smaller, which is highly desirable.
This created 14 strata of establishments for the year 2000 frame based upon 1999 data.
Using the models based upon 1999 data, predictions were produced for the
establishments on the frames for the year 1998 and 2000. Using each of these
predictions, the establishments on these frames were placed into the 14 strata developed
using 1999 models. The establishments in the samples from the years 1998 and 2000
were used to calculate estimates of variance components for each of the strata.
Return to Table of Contents
Using these variance components and variance components calculated using the same
data for the old strata, and counts from the 2000 frame, errors for a variety of allocations
for the new and old strata could be evaluated using the following formula:
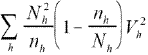
where
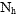is the size of the stratum,
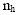is the sample size for the hth stratum, and
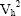is the variance within the hth stratum. Assuming that a typical state has a distribution of
establishments similar to that of the entire country, results could be produced for any
allocation using stratum sizes that are available from the frame and values of the
components of variance that were estimated using the sample data.
Estimates of standard errors were made for two variables: the total number of
establishments offering health insurance and the total number of employees enrolled.
These variables were chosen because they represent the two different types of estimates
made with IC data. The first is driven by numbers of establishments. Such estimates are
dominated by the large number of small establishments on the frame. The second is
dominated by establishments with large employments and enrollments. The former
requires a large sample of small establishments, and the latter requires that the sample be
dominated by large establishments. These two opposite types of variables require a
sampling strategy that in some way balances the sample between numbers of
establishments and numbers of employees.
Several methods have been recommended to accomplish this type of allocation
(Cochran, 1977). One is to produce variance components for each stratum that are
weighted averages of the variance components for each variable for the stratum. A
second is to assign the allocation to the cell as a weighted average of the optimal
allocations for the stratum for the individual variables. Another method, used for the
1993 National Employer Health Insurance Survey, a one-time survey with similar data
needs as the IC, is to allocate sample to strata based upon the measure of size equal to
the square root of the employment at each establishment. This allocation tends to
balance enrollment and numbers of establishments.
The results for several of the allocation tested are shown in Table 1.
Table 1. Standard errors for national trial allocations using old and new strata
| |
Current strata |
Proposed new strata |
| Totals Estimated Allocation |
Establishments offering health insurance |
Number of enrollees |
Establishments offering health insurance |
Number of enrollees |
| Optimal for number of establishments offering health insurance |
15,088 |
4,626,353 |
14,025 |
5,054,792 |
| Optimal for number of enrollees |
25,052 |
840,347 |
27,173 |
388,512 |
| Square root of employment |
19,862 |
1,047,248 |
17,885 |
772,031 |
| Average of the optimal allocations |
17,827 |
997,305 |
16,673 |
471,909 |
| Current |
18,802 |
978,356 |
Inapplicable |
Inapplicable |
The table demonstrates the following:
-
For either strata definition, the optimal Neyman allocations for the individual
variables are very poor for the other type of variable. This demonstrates the need for
a balanced allocation.
-
The square root of the employment allocation and the average of the optimal
allocations both tend to balance the results between the two optimal allocations. The
current allocation also accomplishes that goal.
-
The optimal allocations using the proposed new strata definitions are across the
board lower than those for the current strata definitions. This means that the
potential for a meaningful decrease in variances is possible using the new
stratification method. Also, the average of the optimal allocations using the new
stratification methods is better than the current stratification and allocation methods.
Return to Table of Contents
Given the possibilities for improvements, further research was undertaken to find an
improved allocation given the proposed new strata definitions. As part of this process,
another variable was added to the analysis: the total single employee contribution. This
variable was added because AHRQ decided that many more estimates were being
requested by users that related to employment than to numbers of establishments. Thus,
it was decided to weight the new allocation more towards that type of variable.
One of the results of this analysis was the development of a 15th stratum for the
proposed new set of strata. This is a certainty stratum of approximately 200 of the
largest establishments. Adding such a stratum to the new strata had a significant effect
on results for the two variables correlated with employment. When added to the current
stratification definitions, a certainty stratum had far less effect.
After much analysis, a final allocation method was accepted that was a weighted average
of 50 percent of the optimal allocation for estimates of the number of establishments that
offer health insurance plus 25 percent each of the optimal allocations for the estimates of
the total enrollment and total single contributions. The decision on the final allocation
was based primarily upon the improvement in variance of the estimates compared with
the current sample. However, some allocations that were slightly better than the final
choice were rejected because of the percentage of the sample required from the largest
firms. There was concern that extra burden on these respondents and the potential loss in
response rate was not worth the risk compared with the slightly better forecasted errors
from the allocations.
Table 2 gives results for the final optimal allocation for the three analysis variables
along with results for the current sample allocation and the chosen new allocation.
Table 2. Standard errors for allocations using old and new strata
| Totals Estimated strata, allocation method |
Establishments offering health insurance |
Number of enrollees |
Total single employee contribution |
| New strata without certainties, minimum possible value for each variable |
14,025 |
388,512 |
1.678 x 108 |
| New strata with certainties, minimum possible value for each variable |
14,025 |
354,813 |
1.606 x 108 |
| Old strata, minimum possible value for each variable |
15,088 |
840,347 |
2.746 x 108 |
| New strata, proposed weighted allocation |
16,770 |
408,658 |
1.729 x 108 |
| Old strata, current allocation |
18,802 |
978,346 |
3.535 x 108 |
The first three rows of the table give the standard error that can be obtained with the
optimal allocation for that variable with that stratification. No one allocation can reach
the minimum value for all the variables. However, as one can see in the table, the
proposed weighted allocation using the new strata gives standard errors that are close to
the best possible values for each of the variables and better than the current allocation
for the total number of establishments. The projected improvements in standard errors
from the new stratification and allocation methods, shown in the fourth row, over the
current methods shown in the fifth row, are 11 percent for total establishments offering
health insurance, 58 percent for total enrollment, and 51 percent for total single
employee contributions.
Appendix B gives the overall percentages of the total establishments, total employment,
enrollment, and sample for each of the 15 strata in the new sample design.
Return to Table of Contents
Changes in Restrictions on Maximum Sample Size per Firm
The IC list sample design contains a process that limits the total expected sample of
establishments that can be selected from an individual firm. This was done to limit the
burden on individual respondents. The total burden for the IC includes sample from the
household sample and the list sample. The members of the household are predetermined
in the sense that they are the employers of respondents to the household survey, and
AHRQ cannot control this sample of employers. On the other hand, the list sample is
designed by AHRQ and Census and selected by the Census. Thus, the expected sample
for a firm within this sample can be controlled. Given that the total sample size for the
private sector from the combined household and list samples is about 44,000 private
sector establishments, if samples were selected proportional to firm’s share of total
employment then, given a total employment of 110 million employees in the private
sector, a company with over 100,000 employees could expect to have over 40
(44,000x100,000/110,000,000) establishments in the sample.
To avoid these large samples, the sum of the probabilities of selection for establishments
within the same firm were limited for the list sample. In order to maintain the same
overall sample size, the probabilities of selection for establishments from smaller firms
within the same strata must be increased so the total probabilities of selection within a
stratum remain equal to the allocated sample size. This leads to the situation that, within
a stratum, establishments with about the same expected values for variables, such as
enrollment, can have different selection probabilities and thus different weights. This
leads to an increase in the sampling error.
Given that there was an opportunity to change this restriction on the sample design, an
effort was first made to determine the effect of the current restrictions on sampling
errors. To measure this effect, several types of design effects were calculated using
SUDAAN, a specialized error estimation software for complex surveys. These estimates
allow one to measure the effects on errors of the several different aspects of a sample
design, stratification, clustering, over sampling, and unequal weighting (Research
Triangle Park, 2002). Of particular interest to the current problem is the ability to
measure the design effect of the sample design with and without unequal weighting.
These effects were run for a variety of variables, such as total enrollment, average
premiums and contributions, etc.. While the results varied by variable, in general the
design effect that took into account unequal weighting within each stratum was twice
that when this effect was removed. Thus to lower this effect could result in significant
improvements in the overall errors for many variables.
After considering the distribution of expected sample sizes per firm, before reduction, a
new reduction method was developed that the Census Bureau believed would result in
acceptable sample sizes per firm and would not place an unreasonable burden on firms
nor the IC budget. The key difference in the two methods is that, under the old method,
the maximum expected sample size for all but two large firms was 10 and some type of
downward adjustment was used for any firm with an original expected sample size of
two or more. The new method applies no adjustments to firms with expected sample size
values less than three and allows for a maximum expected number of units of 50. Even
with these lessened restrictions on the list sample, the actual burdens on firms when
combined with dropping the household sample, are decreased overall. The two reduction
methods are shown in Appendix C.
To assess the possible improvement in sampling errors for this method, the following
assessment was performed.
Return to Table of Contents
Within each stratum with N establishments in the IC, an independent sample of size n is
selected. Assuming that each establishment selected has a common mean
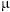and the same variance
 ,
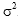then if units are selected with equal probabilities the variance of an estimate
of a total for this variable is
 .
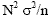In this case, the probability of selection of all
establishments is n/N. If instead, unequal probabilities pf selection are used and the
probability of selection for the ith establishment is written as
 ,
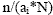then the variance of the estimate is:
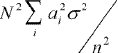
To compare the variance of this estimate with that of the one with equal probability of
selection, we simply calculate the relative value of the variance of the unequal
probability estimate to that of the equal probability of selection estimate by taking the
ratio of the two variances:
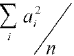
To obtain a rough estimate of the differences in variances, the value of
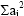for the sample of all firms with more than 1,000 employees was calculated for each method.
This was done assuming that all the establishments were from the same strata and using
the actual values of the expected sample sizes before adjustment from the 2003 IC
sample. The two adjustment methods were applied to the expected samples for the
largest firms. This decreased the expected sample sizes and increased the weights for
these establishments. The expected sample sizes for remaining firms were adjusted
upwards so that the final expected overall sample size was the original value of n. This
then decreased the weights for these establishments. Although these are not the actual
final adjustments because each state has a different stratum for these firms and the strata
could have different values of
,
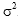it was believed that this would give an idea of the
relative values of the sums versus n for the various adjustment methods.
Using the approach, the current method yields a value of 1.966n. The new method has a
value of 1.218n. The relative magnitude of the two values is 1.61. Applying the square
root to this value yields 1.27. Thus, for estimates for the firms with more than 1,000
employees, the new method of reduction has approximately 27 percent smaller standard
error than similar estimates where the sample was selected using the old method of
burden reduction.
While the reduction method is only one of the reasons that weights are unequal, AHRQ
believes that using the new method will result in significant reductions in standard errors
for most national estimates and estimates made for the groups of firms above 1,000
employees.
Return to Table of Contents
Government Sample Improvements
In surveys prior to the 2003 IC, the sample of governments consisted of two parts, (1) a
set of certainties that included all governments with more than 5,000 full-time equivalent
employees and (2) a sample of smaller governments that was allocated so that
governments in smaller states were over sampled relative to those in larger states. This
happened because, using the old allocation method, the over sampling for smaller states
was applied to both governments and private sector establishments. This was done
because the goal was to produce quality estimates for the set of all employers in the
state, public, and private sector combined. Once each state was given an overall
allocation of private sector establishments and non-certainty governments, the state’s
total allocation was broken proportional to the relative size of the private sector and noncertainty
governments in each state. Because small states were over sampled relative to
large states, then non-certainty governments were also over sampled relative to the same
governments in large states. Assuming similar variances among non-certainty
governments within each of the states, this over sampling would yield a less efficient
sample for estimates at a larger geographic area, such as Census Regions, than a
proportional allocation across all non-certainty government units within all states in the
area.
This over sampling was necessary if there was a demand for estimates for the combined
public and private sector universe within each state. However, users have rarely
requested an estimate of the combination of public and private sector employers. Users
request estimates for the private sector only, and some have requested state estimates for
governments only. By imposing a slightly lower minimum sample for each state for the
private sector as was done in the state-level allocation discussed earlier in this paper,
AHRQ assured that the former would be produced for all states with relatively good
standard errors. Using the past combined allocation, the state estimates for governments
could not be produced with a reasonable error rate except for the largest states, even with
the over sample of non-certainty governments.
Since, with the exception of very large states, good state estimates for the government
sector are not possible with the over sampling of governments in smaller states, it was
decided not to over sample any governments at the state level. Instead, the government
sample for the non-certainty governments was redesigned as follows:
-
All state governments were defined as a certainty sample unit.
-
All local governments with more than 5,000 full-time equivalent employees
according to the Census of Governments were defined as a certainty sample unit.
-
Each of the nine Census Divisions was allocated 200 non-certainty government
sample units.
The first two items were part of the old government sample design for the IC from 1996
to 2002. The final allocation gives the same total national allocation for non-certainty
governments as in past surveys. The totals within Census Divisions are also
approximately equal to the past allocations at the Census Division level. However,
within Census Divisions, the allocation for non-certainty governments is proportional to
the government employment in each state. The effect of this change should be to
improve the published estimates for each Census Division, since the allocation of the
small sample size for each Census Division is now done optimally for each Census
Division. This is because there is no over sampling within Census Divisions by state as
before. The allocations are proportional to state size within Census Divisions. This
increases the sample of the larger states that have the most government employment.
Making better estimates for each Census Division also will improve national estimates
for the government sector. This will also allow AHRQ to make better state-level
estimates for the larger states where quality estimates are possible.
Return to Table of Contents
Summary
In summary, several major changes are being implemented for the 2004 MEPS-IC sample:
-
The overall sample for the private sector is being increased to allow for state-level
estimates for all 50 states and the District of Columbia. This is an improvement over
the current sample for which estimates were produced for 40 states. Due to the
increased sample, this over sampling of 11 more states should not affect the quality
of the national estimates.
-
An improved stratification and allocation process is being implemented for the
private sector. This should lead to improved estimates at the state level using the
same sample size. Better state estimates will also mean better national estimates.
-
A change is being made to the process that limits the sample for individual firms.
The new process will not limit sample for individual firms as severely and should
reduce the error for private sector estimates made for firms with over 1,000
employees. It should also reduce errors for private sector estimates made for the
entire population. This should be true for state- and national-level estimates.
-
Finally, the non-certainty government sample has been changed to an optimal
allocation within each Census Division. This should improve both national and
Census Division government estimates. This allocation should also improve
estimates for some of the largest states where an estimate can be made.
Taken together, the IC will soon produce significantly better state and national estimates
for the private sector, and there will be quality estimates for all states, rather than just 40
states. These improvements should occur for all variables and for estimates for all
subnational and substate cells. There should also be improvements in estimates for the
nation, Census Divisions, and the largest states for government results.
Return to Table of Contents
References
Cochran WG. Sampling techniques. New York: John Wiley and Sons; 1977.
Cohen S. Sample Design of the 1996 Medical Expenditure Panel Survey Household
Component. Rockville(MD); Agency for Health Care Policy and Research; 1997. MEPS
Methodology Report No. 2. AHCPR Pub No. 97-0027.
Kish L. Survey sampling. New York: John Wiley and Sons; 1965.
Marker D, Bryant E, Wallace L, Yansaneh L. National Employee Health Insurance
Survey (NEHIS): Draft final methodology report, Volume I: Statistical Methodology.
Rockville, (MD): Westat, Inc.: 1996.
MEPS Insurance Component: Technical Notes and Survey Documentation. Agency for
Healthcare Research and Quality, Rockville, MD.
http://www.meps.ahrq.gov/mepsweb/survey_comp/ic_technical_notes.shtml
Research Triangle Institute. SUDAAN User’s Manual, Release 8.0. Research Triangle
Park, NC: Research Triangle Institute; 2002.
Sommers JP. List sample design of the 1996 Medical Expenditure Panel Survey
Insurance Component. Rockville (MD): Agency for Health Care Policy and Research;
1999. MEPS Methodology Report No. 6 Pub. No. 99-0037.
Return to Table of Contents
Appendix A. Private Sector Allocations and Response per State
Return to Table of Contents
| State |
Private sector
sample |
Expected private
sector response |
| Alabama |
761 |
560 |
| Alaska |
704 |
520 |
| Arizona |
761 |
560 |
| Arkansas |
761 |
560 |
| California |
2842 |
2038 |
| Colorado |
761 |
560 |
| Connecticut |
761 |
560 |
| Delaware |
704 |
520 |
| District of Columbia |
704 |
520 |
| Florida |
1274 |
925 |
| Georgia |
761 |
560 |
| Hawaii |
704 |
520 |
| Idaho |
704 |
520 |
| Illinois |
1139 |
829 |
| Indiana |
761 |
560 |
| Iowa |
761 |
560 |
| Kansas |
761 |
560 |
| Kentucky |
761 |
560 |
| Louisiana |
761 |
560 |
| Maine |
761 |
560 |
| Maryland |
761 |
560 |
| Massachusetts |
761 |
560 |
| Michigan |
846 |
625 |
| Minnesota |
761 |
560 |
| Mississippi |
761 |
560 |
| Missouri |
761 |
560 |
| Montana |
704 |
520 |
| Nebraska |
761 |
560 |
| Nevada |
761 |
560 |
| New Hampshire |
761 |
560 |
| New Jersey |
809 |
595 |
| New Mexico |
761 |
560 |
| New York |
1738 |
1255 |
| North Carolina |
761 |
560 |
| North Dakota |
704 |
520 |
| Ohio |
967 |
707 |
| Oklahoma |
761 |
560 |
| Oregon |
761 |
560 |
| Pennsylvania |
1021 |
746 |
| Rhode Island |
704 |
520 |
| South Carolina |
761 |
560 |
| South Dakota |
704 |
520 |
| Tennessee |
761 |
560 |
| Texas |
1637 |
1184 |
| Utah |
761 |
560 |
| Vermont |
704 |
520 |
| Virginia |
761 |
560 |
| Washington |
761 |
560 |
| West Virginia |
761 |
560 |
| Wisconsin |
761 |
560 |
| Wyoming |
704 |
520 |
| Certainty establishments (not assigned by state) |
100 |
90 |
| Total |
43708 |
32070 |
Appendix B. Percent of Universe and Sample
per Stratum: Private Sector
| Stratum |
|
Percent of
establishments |
Percent of
employment |
Percent of
enrollment |
Percent of
sample |
| Probability of offering
health insurance |
Total enrollment
per establishment |
|
|
|
|
| Less than 25% |
very low |
13.4 |
2.3 |
1.6 |
10.8 |
| 25% to 40% |
very low |
14.7 |
3.4 |
2.4 |
11.8 |
| 40% to 58% |
very low |
13.6 |
4.5 |
3.5 |
14.7 |
| 58% to 75% |
low |
11.3 |
2.4 |
2.4 |
10.2 |
| 58% to 75% |
medium |
2.8 |
3.7 |
2.6 |
2.1 |
| 75% to 90% |
low |
10.1 |
2.0 |
2.2 |
10.4 |
| 75% to 90% |
medium |
5.7 |
4.1 |
3.9 |
2.7 |
| 75% to 90% |
high |
1.0 |
3.6 |
2.7 |
1.2 |
| Above 90% |
very low |
13.7 |
5.1 |
4.3 |
8.7 |
| Above 90% |
low |
7.6 |
9.8 |
9.4 |
5.4 |
| Above 90% |
medium |
3.7 |
11.5 |
11.4 |
4.6 |
| Above 90% |
high |
1.9 |
12.3 |
12.5 |
3.8 |
| Above 90% |
very high |
0.9 |
11.4 |
12.6 |
3.1 |
| Above 90% |
highest |
0.5 |
21.7 |
25.9 |
10.5 |
| Certain |
highest |
negligible |
2.1 |
2.5 |
negligible |
Return to Table of Contents
Appendix C. Methods for Reduction of Expected Sample for Private
Sector Firms
Current Method
Let sump equal the original expected sample for a firm and sumf be the final, then the
algorithm to reduce the value for certain firms is:
| If sump > 50 then sumf = 15 |
| if 20 < sump=< 50 then sumf = 10 |
| if 6 < sump <= 20 the sumf = .5*sump |
| if 3 < sump <= 6 then sumf = 3 |
| and if 1 < sump <=3 then sumf = 1. |
New Method
| If 0 < sump < 3 the sumf = sump |
| if 3<=sump < 6 then sumf = 3 + (2/3)*(sump - 3) |
| if 6<=sump < 12 then sumf = 5 + (½)*(sump - 6) |
| if 12<=sump < 36 then sumf = 8 + (1/3)*(sump - 12) |
| if 36<=sump then sumf = 16 + (2/3)*(sump - 36) |
Return to Table of Contents
Return to the MEPS Homepage
Suggested Citation:
Sommers, J. P. Updates to the Medical Expenditure Panel Survey Insurance
Component List Sample Design, 2004. Methodology Report No. 18. January
2007. Agency for Healthcare Research and Quality, Rockville, Md. http://www.meps.ahrq.gov/mepsweb/data_files/publications/mr18/mr18.shtml |
Back
Email Updates