Methodology Report #16:
Producing State Estimates with the Medical Expenditure Panel Survey, Household Component
John P. Sommers, PhD, Agency for Healthcare Research and Quality.
Table of Contents
Abstract
The Medical Expenditure Panel Survey (MEPS)
Background
Need for State Estimates from the MEPS-HC
State Estimates with MEPS-HC Data
The MEPS-HC
Number of PSUs
Design-based state estimates
Design-based estimates with weights post-stratified by state
Composite estimation
Conclusions and Recommendations
Acknowledgments
References
Abstract
In recent years, there has been a growing need for
estimates of health care expenditures at the state level. The Household
Component of the Medical Expenditure Panel Survey (MEPS-HC) is a survey
designed to collect information on and to produce national and regional
estimates of health care expenditures. However, while the sample design
allows for some state estimates to produced, there is no assurance that
the quality of these estimates are adequate for use, since the original
purpose of the survey did not include production of state estimates.
This paper describes the results of research using data
from the MEPS-HC to produce a selected group of state-level estimates
for the 30 states with the largest populations. Three methods of
estimation are used. Each method is evaluated using standard measures,
and conclusions about the quality of these estimates, along with
recommendations, are given.
The estimates in this report are based on the most
recent data available at the time the report was written. However,
selected elements of MEPS data may be revised on the basis of additional
analyses, which could result in slightly different estimates from those
shown here. Please check the MEPS Web site for the most current file
releases.
Center for Financing, Access, and Cost Trends
Agency for Healthcare Research and Quality
540 Gaither Road
Rockville, MD 20850
www.meps.ahrq.gov
The Medical Expenditure Panel Survey (MEPS)
Background
The Medical Expenditure Panel Survey (MEPS) is conducted
to provide nationally representative estimates of health care use,
expenditures, sources of payment, and insurance coverage for the U.S.
civilian noninstitutionalized population. MEPS is cosponsored by the
Agency for Healthcare Research and Quality (AHRQ), formerly the Agency
for Health Care Policy and Research, and the National Center for Health
Statistics (NCHS).
MEPS comprises three component surveys: the Household
Component (HC), the Medical Provider Component (MPC), and the Insurance
Component (IC). The HC is the core survey, and it forms the basis for
the MPC sample and part of the IC sample. Together these surveys yield
comprehensive data that provide national estimates of the level and
distribution of health care use and expenditures, support health
services research, and can be used to assess health care policy
implications.
MEPS is the third in a series of national probability
surveys conducted by AHRQ on the financing and use of medical care in
the United States. The National Medical Care Expenditure Survey (NMCES)
was conducted in 1977, the National Medical Expenditure Survey (NMES) in
1987. Beginning in 1996, MEPS continues this series with design
enhancements and efficiencies that provide a more current data resource
to capture the changing dynamics of the health care delivery and
insurance system.
The design efficiencies incorporated into MEPS are in
accordance with the Department of Health and Human Services (DHHS)
Survey Integration Plan of June 1995, which focused on consolidating
DHHS surveys, achieving cost efficiencies, reducing respondent burden,
and enhancing analytical capacities. To accommodate these goals, new
MEPS design features include linkage with the National Health Interview
Survey (NHIS), from which the sample for the MEPS-HC is drawn, and
enhanced longitudinal data collection for core survey components. The
MEPS-HC augments NHIS by selecting a sample of NHIS respondents,
collecting additional data on their health care expenditures, and
linking these data with additional information collected from the
respondents’ medical providers, employers, and insurance providers.
Household Component
The MEPS-HC, a nationally representative survey of the
U.S. civilian noninstitution-alized population, collects medical
expenditure data at both the person and household levels. The HC
collects detailed data on demographic characteristics, health
conditions, health status, use of medical care services, charges and
payments, access to care, satisfaction with care, health insurance
coverage, income, and employment.
The HC uses an overlapping panel design in which data
are collected through a preliminary contact followed by a series of five
rounds of interviews over a two and a half year period. Using
computer-assisted personal interviewing (CAPI) technology, data on
medical expenditures and use for two calendar years are collected from
each household. This series of data collection rounds is launched each
subsequent year on a new sample of households to provide overlapping
panels of survey data and, when combined with other ongoing panels, will
provide continuous and current estimates of health care expenditures.
The sampling frame for the MEPS-HC is drawn from
respondents to NHIS, conducted by NCHS. NHIS provides a nationally
representative sample of the U.S. civilian noninstitutionalized
population, with oversampling of Hispanics and blacks.
Medical Provider Component
The MEPS-MPC supplements and validates information on
medical care events reported in the MEPS-HC by contacting medical
providers and pharmacies identified by house-hold respondents. The MPC
sample includes all hospitals, hospital physicians, home health
agencies, and pharmacies reported in the HC. Also included in the MPC
are all office-based physicians:
- Providing care for HC respondents receiving Medicaid.
- Associated with a 75 percent sample of households receiving care
through an HMO (health maintenance organization) or managed care plan.
- Associated with a 25 percent sample of the remaining households.
Data are collected on medical and financial characteristics of medical and pharmacy events
reported by HC respondents, including:
- Diagnoses coded according to ICD-9 (9th Revision, International
Classification of Diseases) and DSMIV (Fourth Edition, Diagnostic and Statistical Manual
of Mental Disorders).
- Physician procedure codes classified by CPT-4 (Current Procedural
Terminology, Version 4).
- Inpatient stay codes classified by DRG (diagnosis related group).
- Prescriptions coded by national drug code (NDC), medication names,
strength, and quantity dispensed.
- Charges, payments, and the reasons for any difference between
charges and payments.
The MPC is conducted through telephone interviews and
mailed survey materials.
Insurance Component
The MEPS-IC collects data on health insurance plans
obtained through private and public sector employers. Data obtained in
the IC include the number and types of private insurance plans offered,
benefits associated with these plans, premiums, contributions by
employers and employees, and employer characteristics.
Establishments participating in the MEPS-IC are selected
through three sampling frames:
- A list of employers or other insurance providers identified
by MEPS-HC respondents who report having private health insurance at the Round 1 interview.
- A Bureau of the Census list frame of private-sector business
establishments.
- The Census of Governments from the Bureau of the Census.
To provide an integrated picture of health insurance,
data collected from the first sampling frame (employers and other
insurance providers) are linked back to data provided by the MEPS-HC
respondents. Data from the other three sampling frames are collected to
provide annual national and State estimates of the supply of private
health insurance available to American workers and to evaluate
policy issues pertaining to health insurance. Since 2000, the Bureau of
Economic Analysis has used national estimates of employer contributions
to group health insurance from the MEPS-IC in the computation of Gross
Domestic Product (GDP).
The MEPS-IC is an annual panel survey. Data are
collected from the selected organizations through a prescreening
telephone interview, a mailed questionnaire, and a telephone follow-up
for nonrespondents.
Survey Management
MEPS data are collected under the authority of the
Public Health Service Act. They are edited and published in accordance
with the confidentiality provisions of this act and the Privacy Act.
NCHS provides consultation and technical assistance.
As soon as data collection and editing are completed,
the MEPS survey data are released to the public in staged releases of
summary reports and microdata files. Summary reports are released as
printed documents and electronic files. Microdata files are released on
CD-ROM and/or as electronic files.
Printed documents and CD-ROMs are available through the
AHRQ Publications Clearinghouse. Write or call:
AHRQ Publications Clearinghouse
Attn: (publication number)
P.O. Box 8547 Silver Spring, MD 20907
800-358-9295
703-437-2078 (callers outside the United States only)
888-586-6340 (toll-free TDD service; hearing impaired only)
To order online, send an e-mail to: ahrqpubs@ahrq.gov.
Be sure to specify the AHRQ number of the document or
CD-ROM you are requesting. Selected electronic files are available
through the Internet on the MEPS Web site:
http://www.meps.ahrq.gov/
For more information, visit the MEPS Web site or e-mail
mepspd@ahrq.gov.
Return to Table of Contents
Background
An investigation of results produced from large-scale
Federal household surveys, reveals few state estimates produced from
these surveys. The exception is the Current Population Survey (CPS),
conducted by the Census Bureau and sponsored by the Bureau of Labor
Statistics, which is the source of state income, poverty, and health
care uninsurance rate estimates (Census Bureau Web site: c). However,
the state personal income and uninsurance rate estimates are
multiple-year averages produced from combining several years of data (DeNavas-Walt
et al., 2004). County- and state-level estimates of income and poverty
are produced using special small area estimation techniques using CPS
and other data. State estimates are rare, and design-based one-year
estimates do not seem to be routinely published. State-level estimates
are not routinely produced from other large-scale Federal household
surveys, including the following:
-
The National Health Interview Survey (NHIS), sponsored by the Centers
for Disease Control and Prevention's National Center for Health
Statistics (NCHS) and conducted by the Census Bureau (NCHS Web site and
Botman, et al., 2000)
-
The Survey of Income and Program Participation (SIPP), conducted by the
Census Bureau (Census Bureau Web site: a and Kostanich and Dippo, 2002)
-
The American Housing Survey (AHS), sponsored by the Department of Housing
and Urban Development and conducted by the Census Bureau (Census
Bureau Web site: b and Census Bureau Web site: d )
-
The Household Component of the Medical Expenditure Panel Survey (MEPS-HC),
sponsored by the Agency for Healthcare Research and Quality (AHRQ)
(Medical Expenditure Panel Survey Web site and Cohen, 2000).
A basic indication explaining why state-level estimates
are not produced with these surveys can be found in the estimates that
are produced with the CPS data by the Census Bureau. Multiyear averages
and small area estimation techniques are used when the reliability of
the design-based estimates is poor. Multiyear averages increase sample
sizes and thus lower errors. Small area estimation techniques use
modeling and other complex and time-intensive estimation methods to "borrow
strength" from data outside the state or outside the survey to improve
results with poor precision that are produced using design-based survey
estimation techniques, such as weighted means and totals. (Ghosh and Rao,
1994)
For the large national Federal surveys, unbiased
design-based estimates for states are possible. An unbiased estimate of
the state average for any variable is simply the weighted sum of the
variable for all sample units within the state divided by the sum of the
weights for the sample units within the state (Cochran, 1977). There are
two reasons, however, why design-based estimates for individual states
are generally of poor precision for the large
national surveys. The first reason is that to meet population sub-domain
and for key survey estimates for specified proportions, the survey
sample sizes are generally allocated on a national basis. For general
population-based national surveys, survey budgets do not allow adequate
sample size in each state to produce state estimates with acceptable
precision. There is generally no focus on state estimates, thus no
minimum state samples. Even for surveys with state-level stratification
as a design feature, such as the NHIS, given that the top10 states have
over half the population, the sample sizes for the remaining states can
fall below an ideal sample size.
Aside from the possible lack of adequate sample sizes in
states, the sample designs used in the surveys listed above also make it
difficult to produce high-quality design-based estimates for states. All
the surveys have stratified multistage cluster sample designs. This
involves sampling of clusters, sets of counties. This limits the samples
in each state, no matter how many persons are in the final sample, to a
limited number of counties within each state. This is done because of
the costs of personal household visits to collect the information if the
sample of persons were spread widely and evenly across the entire
country. This clustering of the sample can have a large impact on the
sampling error. If the average values for the variables being estimated
vary considerably across the clusters of counties, then the sampling
error is effectively limited by the number of county clusters. For
further detail on the variances of cluster samples, see Cochran, 1977.
Return to Table of Contents
Need for State Estimates from the MEPS-HC
In 2004, the increase in costs of health insurance was
above 10 percent (Kaiser Family Foundation, 2004). Further, large
numbers of persons are without health coverage (DeNavas-Walt et al.,
2004). At the same time, state budgets have been hard hit by loss of
revenues and increasing health care costs from Medicaid spending. In
2003, Medicaid spending increased 8 percent over 2002 levels and was
21.4 percent of all state spending. As a result, most states reduced
Medicaid benefits, reduced Medicaid eligibility, and implemented
prescription drug cost control programs for Medicaid (National
Association of State Budget Officers, 2003).
Given the variety of methods being implemented by the
states to control Medicaid and other health costs and to increase the
number of persons with health insurance, it is of great interest for all
states to know which efforts have succeeded and which have not. To
assess these results, one must have reliable data. Health care usage and
costs at the state level must be analyzed to determine if costs are
increasing over time and if more people are using health care. It would
also be of use to know who is using care and what types; for instance,
how much care certain parts of the population use and what type, doctor
visits, hospitals, etc.
Because of these data needs, there is an emerging drive
within the Department of Health and Human Services (DHHS) to examine the
feasibility of producing state data from population-based surveys and
other sources. This paper examines the possibility of producing selected
state estimates from one core DHHS data source.
Return to Table of Contents
State Estimates with MEPS-HC Data
The MEPS-HC
National estimates of health care expenditures are an
important resource for health policymakers and health services
researchers. MEPS collects information regarding the use and payment for
health care services from a nationally representative sample of the U.S.
civilian noninstitutionalized population. In addition to the annual
nationally representative expenditures estimates from MEPS, there is a
growing need for estimates at the subnational level. While MEPS was
designed to ensure reliable estimates at the national and regional level
for individuals, families, and selected population subgroups, recent
research has focused on the capacity for subnational estimates. A 2004
MEPS Statistical Brief (Machlin, et al., 2004) provided estimates of
health care expenses and uninsured rates for the U.S. community
population under age 65 in 10 large metropolitan areas. This paper
examines the capacity for producing expenditure estimates with
acceptable precision at the state level using MEPS.
The sample of households for the MEPS-HC is a subsample
of households that responded to the prior year's NHIS. The MEPS sample is
drawn from approximately one-half of the primary sampling units (PSUs)
in the NHIS. Oversampling of households with Hispanics and African
Americans carries over from the NHIS to the MEPS sample design. In
addition, in forming strata for selection of the first-stage sampling
units or PSUs in the NHIS, state was used as a stratification variable.
This design feature carries over from the NHIS to MEPS-HC since the MEPS-HC
uses approximately half of the NHIS PSUs. In this paper, the MEPS-HC
design is investigated with respect to its capacity to support reliable
state-level estimates for a selected number of states.
Return to Table of Contents
Number of PSUs
The first issue one must address when trying to make
state estimates from a survey with a cluster sample is the number of
PSUs available to make the estimates for each state. If the between PSU
variance is large compared with the within PSU variance, a very small
number of PSUs means a large error, regardless of the number of final
stage sampling units (Cochran, 1977). For this reason, we checked the
PSU structure for the MEPS. We found that if we ranked states by total
population that the 10 largest states each had either more than six PSUs
and/or had a number of certainty PSUs that covered a large portion (60
percent or more) of the state population. For the second largest set of
states, those with population ranks from 11 through 20, the states
contained at least four PSUs and/or had a certainty PSU that covered a
large portion of the state population. For states with population ranks
from 21 through 30, the minimum number of PSUs was three, but most had
four or more non-certainty PSUs and population coverage of the selected
PSUs was limited. However, since there are enough PSUs to calculate an
error for each of these states, this third set of states is also used in
the analysis. Most of the remaining small states had either one or no
PSUs, and these were not included in the analysis.
Return to Table of Contents
Design-based state estimates
The first step of the research was to develop simple
design-based estimates using the MEPS-HC design structure and data for
2002 for six types of expenditures: total (all types combined), dental
visits, inpatient facility stays, office-based visits, outpatient
doctor visits, and prescription drugs. This was done
using the weights that were created by post-stratification to national
CPS values for cells defined by age, race, gender, and marital status.
For each type of expenditure, an estimate for each state was made for
the percentage of persons who had that expenditure, the mean for those
who had an expenditure, and the total expenditures. These estimates were
created for each of the 30 largest states defined by total population.
Relative standard error results were averaged for each type of estimate
for three state groups: the 10 largest states, the second 10 largest
states, and the third 10 largest states. These are called groups 1, 2,
and 3 in order from the largest to smallest states. Results are shown in
table 1. Maximum relative standard errors in each group are also shown.
The standard errors for the estimates shown in the
tables in this report were produced using a set of 64 partially balanced
half samples and the balanced repeated replication method (Wolter, 1985).
This was done to take into account the post-stratification done to the
sampling weights. For variance estimation purposes, the weights were
post-stratified for each replicate. We found that use of Taylor Series
methods for this first set of design-based estimates gave similar
results. However, this was not true for results produced and discussed
latter in this paper and shown in tables 2 and 3.
Table 1. Average and maximum relative standard errors (RSEs) by state size group for typical estimates: National post-stratification
| |
|
Conditional mean
expenditures |
Percent of persons
with expenditure |
Total
expenditures |
Expenditure
type |
Size
group |
Mean
RSE |
Max
RSE |
Mean
RSE |
Max
RSE |
Mean
RSE |
Max
RSE |
| All types combined |
1 |
0.0989 |
0.1697 |
0.0226 |
0.0327 |
0.2159 |
0.3437 |
| All types combined |
2 |
0.1602 |
0.3223 |
0.0291 |
0.0424 |
0.3336 |
0.5232 |
| All types combined |
3 |
0.1677 |
0.3377 |
0.0389 |
0.1007 |
0.4120 |
0.5737 |
| Dental visits |
1 |
0.1423 |
0.2361 |
0.0713 |
0.1035 |
0.2387 |
0.3130 |
| Dental visits |
2 |
0.1453 |
0.2528 |
0.0947 |
0.1538 |
0.3484 |
0.5089 |
| Dental visits |
3 |
0.2499 |
0.5821 |
0.1272 |
0.2031 |
0.4438 |
0.6494 |
| Inpatient facility |
1 |
0.2110 |
0.4049 |
0.1299 |
0.1834 |
0.2928 |
0.4152 |
| Inpatient facility |
2 |
0.2920 |
0.5901 |
0.2056 |
0.3031 |
0.4618 |
0.7730 |
| Inpatient facility |
3 |
0.3495 |
0.8165 |
0.2404 |
0.4383 |
0.5629 |
0.7007 |
| Office based visits |
1 |
0.1091 |
0.1621 |
0.0330 |
0.0514 |
0.2138 |
0.3180 |
| Office based visits |
2 |
0.1417 |
0.2558 |
0.0468 |
0.0765 |
0.3212 |
0.4930 |
| Office based visits |
3 |
0.1899 |
0.2571 |
0.0603 |
0.1372 |
0.4060 |
0.5495 |
| Outpatient doctors |
1 |
0.1746 |
0.2661 |
0.1231 |
0.1761 |
0.2782 |
0.4306 |
| Outpatient doctors |
2 |
0.338 |
0.6895 |
0.2111 |
0.3783 |
0.4673 |
0.7005 |
| Outpatient doctors |
3 |
0.3764 |
0.7446 |
0.2794 |
0.4949 |
0.5280 |
0.7346 |
| Prescription drugs |
1 |
0.0953 |
0.1923 |
0.0389 |
0.0532 |
0.2305 |
0.4494 |
| Prescription drugs |
2 |
0.1290 |
0.2104 |
0.0531 |
0.0912 |
0.3401 |
0.531 |
| Prescription drugs |
3 |
0.1696 |
0.2695 |
0.0667 |
0.1392 |
0.4025 |
0.5868 |
Source: AHRQ, Household Component of the Medical Expenditure Panel Survey, 2002
Table 1 shows
-
State-level estimates with acceptable
precision can be made for some states from the MEPS-HC, but there are
still many estimates of poor precision. This can be seen from the
maximum RSE values for many of the groups. (Note: RSE ge 0.30 is
considered as poor.)
-
Estimates for the percentage of persons
with each type of expenditure have good precision, while the total
expenditure estimates are of uniformly poor quality.
-
The estimates are generally of best
quality for expenditure types that affect the most people and thus
have the greatest sample, such as all types combined or office-based
visits, while the worst are inpatient facility and outpatient doctor
estimates because the numbers of sample persons with these expenditure
types are very small. None of the size groups of states could be
published for the latter two types of expenditures.
-
The estimates decline in precision as the
size of states decreases.
-
With a goal of a maximum RSEs of 20
percent, for the majority of the cases only estimates for the 10
largest states could be produced.
Most of these results with respect to the reliability of
the estimates could be expected. Most are directly related to expected
sample. For any type of expenditure, the percentage of persons with an
expenditure is the best estimate because this estimate is based upon the
entire sample and the distribution. The conditional mean and total
expenditure estimates are based upon subsets of the sample in each
state. Further, these estimates are based upon the distribution of
expenditures which can be highly skewed. The extremely poor quality of
the total expenditure estimates versus the conditional mean estimates
can be attributed to the fact that the between PSU variances of
population totals are much higher than the between PSU variances of
average usage.
Return to Table of Contents
Design-based estimates
with weights post-stratified by state
After review of the first set of results, it was decided
that the estimates could be improved using weights that were
post-stratified to CPS population totals at the state level. For each
state, the nonresponse adjusted weights were post-stratified by state,
age, race, and gender. The use of these weights produced a marked
improvement in the precision of the results.
Table 2. Average and maximum relative standard errors (RSEs) by state size group for typical estimates: State level post-stratification
| |
|
Conditional mean
expenditures |
Percent of persons
with expenditure |
Total
expenditures |
Expenditure
type |
Size
group |
Mean
RSE |
Max
RSE |
Mean
RSE |
Max
RSE |
Mean
RSE |
Max
RSE |
| All types combined |
1 |
0.0744 |
0.1126 |
0.0152 |
0.0206 |
0.0756 |
0.1181 |
| All types combined |
2 |
0.1072 |
0.2112 |
0.0198 |
0.0283 |
0.1085 |
0.2179 |
| All types combined |
3 |
0.1250 |
0.2635 |
0.0256 |
0.0558 |
0.1340 |
0.2582 |
| Dental visits |
1 |
0.1128 |
0.2032 |
0.0512 |
0.0794 |
0.1288 |
0.2214 |
| Dental visits |
2 |
0.1123 |
0.1947 |
0.0703 |
0.1050 |
0.1252 |
0.1974 |
| Dental visits |
3 |
0.1804 |
0.4529 |
0.0921 |
0.1366 |
0.1988 |
0.4655 |
| Inpatient facility |
1 |
0.1631 |
0.2852 |
0.0972 |
0.1482 |
0.1759 |
0.2896 |
| Inpatient facility |
2 |
0.2229 |
0.5188 |
0.1427 |
0.2009 |
0.2738 |
0.5763 |
| Inpatient facility |
3 |
0.2591 |
0.6084 |
0.1870 |
0.3432 |
0.3183 |
0.6300 |
| Office based visits |
1 |
0.0869 |
0.1217 |
0.0227 |
0.0349 |
0.0887 |
0.1252 |
| Office based visits |
2 |
0.1037 |
0.1751 |
0.0335 |
0.0589 |
0.1112 |
0.1827 |
| Office based visits |
3 |
0.1376 |
0.2090 |
0.0429 |
0.0829 |
0.1564 |
0.2494 |
| Outpatient doctors |
1 |
0.1399 |
0.2267 |
0.0883 |
0.1278 |
0.1574 |
0.2294 |
| Outpatient doctors |
2 |
0.2406 |
0.3997 |
0.1561 |
0.2291 |
0.2717 |
0.3809 |
| Outpatient doctors |
3 |
0.2546 |
0.4987 |
0.2078 |
0.3453 |
0.3061 |
0.6082 |
| Prescription drugs |
1 |
0.0674 |
0.1496 |
0.0254 |
0.0357 |
0.0743 |
0.1534 |
| Prescription drugs |
2 |
0.0890 |
0.1529 |
0.0349 |
0.0582 |
0.0976 |
0.1592 |
| Prescription drugs |
3 |
0.1235 |
0.2644 |
0.0418 |
0.1015 |
0.1353 |
0.2463 |
Source: AHRQ, Household Component of the Medical Expenditure Panel Survey, 2002
The use of weights post-stratified with state population
totals yielded the following results shown in table 2:
- Results are uniformly better than those
in table 1.
- Of special interest are the results for
total expenditures for each type. These estimates are now of
approximately the same quality as those for the conditional mean
expenditures for the same type of expenditure. This improvement is
likely the result of the stabilization of totals from the use of
state-specific post-stratification. This post-stratification
essentially makes the estimates of totals a ration estimate which uses
the average usage times the mean conditional expenditure times an
outside population total for each state. As we saw earlier, the RSEs
of average usage and mean conditional expenditure estimates were more
precise, and this change in the estimates of total expenditures
results in estimates with RSEs closer to those of the first two types
of estimates. Nevertheless, there are still estimates with very large
RSEs.
- Although improved, estimates for inpatient
facility and outpatient doctors are still problematic.
- For all other expenditure groups, all
types combined, office-based visits, dental visits, and prescription
drugs, the improvements are such that one could make estimates for the 20
largest states in size groups 1 and 2, with very few estimates with an
RSE greater than 20 percent.
Estimates in an AHRQ report titled
Estimates of Health Care Expenditures for the 10 Largest States, 2002,
are based on this methodology (Machlin and Sommers, 2005).
Return to Table of Contents
Composite estimation
Given that we have produced estimates for every state, a
small area estimation approach could potentially be used to adjust and
improve these estimates by "borrowing strength across states." In this
case, one can consider a random effects model or a Bayesian approach
based upon such a model (Ghosh and Rao, 1994). However, it was decided
to use a method that makes no assumptions about the relationships among
estimates and is simple to apply across a large number of estimates.
It was decided to apply a composite estimation technique
to estimates of the conditional mean expenditures and percentages with
an expenditure. Strength can be borrowed from sample estimates at the
Census Division level, the regional level, or the national level. This
type of estimate uses a weighted average
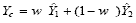
where
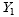 and
and
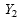 are usually a synthetic and direct estimates of the same
item. The weight is determined by minimizing the mean squared error (MSE)
of the linear combination of estimators. In this case, the sample Census
Division estimate for a larger geographic area was chosen as the
synthetic estimate and the state estimate as the direct estimate. The
Division estimates were chosen as the synthetic estimate because there
seemed to be good correlation between estimates of states within the
same Division. Thus, it seemed that the other states in the Division
would be most helpful in providing information and strength for one
another within the Division. Under these conditions, assuming that the
state estimate is an unbiased estimate of the state value, then the
value of w which minimizes the MSE of the composite estimator is
are usually a synthetic and direct estimates of the same
item. The weight is determined by minimizing the mean squared error (MSE)
of the linear combination of estimators. In this case, the sample Census
Division estimate for a larger geographic area was chosen as the
synthetic estimate and the state estimate as the direct estimate. The
Division estimates were chosen as the synthetic estimate because there
seemed to be good correlation between estimates of states within the
same Division. Thus, it seemed that the other states in the Division
would be most helpful in providing information and strength for one
another within the Division. Under these conditions, assuming that the
state estimate is an unbiased estimate of the state value, then the
value of w which minimizes the MSE of the composite estimator is
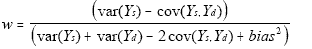
where s denotes the design-based state estimator and d
the division estimator for the larger geographic area. Bias squared in
this case is the squared difference in expected values of the state and
synthetic estimates:
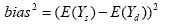
This result can be obtained simply by taking the MSE of
the composite estimate and using differentiation to calculate the value
of w which minimizes the result.
The terms in the numerator can be estimated using the
half samples. The bottom term can be estimated using the square of the
difference of the two estimators. However, that estimate can be very
unstable. Thus, a method using the sum of squared differences of the
half sample estimates was developed to estimate the denominator term,
which is the variance of the difference of the two estimators plus the
squared difference in their expected values. Using these estimates for
w, new estimates and their MSEs and RSEs were calculated using
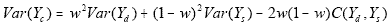
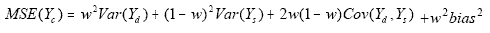
This MSE was estimated using the individual parts
developed in the calculation of w. Of special interest is the estimate
of the bias. One can use the fact that
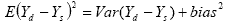
One can just take the difference of the two estimates
squared and subtract an estimate of the variance of the difference of
the two estimates to obtain an estimate of the bias. However, this is an
unstable estimate. We instead take advantage of the following expected
value for the difference of the two estimates for the ith half sample:
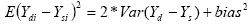
Thus we average the values of the difference squared for
each half sample and subtract the standard estimate of twice the
variance to obtain an estimate of the bias.
Because the value of w is an estimate, the sample
estimate of this variance is only an estimate of the variance of the
estimator given the estimate of w. This does not account for the
expected variance due to the estimation of w. To account for this
variation, w was estimated using groups of half samples. Specifically, w
was estimated using these sets of half samples and half sample estimates
of the composite were made by varying the estimates of w with the full
sample values of the model and division estimates. Addition of this term
was prompted by bias found by Prassad and Rao (1990) in formulas that
did not consider the variation caused by estimation of w. This term did
not add large sums to the overall errors. This indicates that the
estimates of variance and bias are generally stable. However, when the
value of w was very close to 1 or 0, the estimates of w became less
stable. It was decided that the value of w would be limited to values
between .1 and .9 for the final composite estimates currently produced.
Return to Table of Contents
Table 3 below shows values obtained using the composite
estimation technique, comparable to those in tables 1 and 2 for
conditional mean expenditures and percentage with the expenditure type.
This synthetic estimate was chosen because it gave better results than
using the Census Division and about the same quality as combining state
and national estimates while not changing the original value of the
state estimates to the same degree as using the national estimates as
the synthetic estimate.
We should note that as with any set of error estimates
made using sampling data, the estimates of mean squared errors used have
errors also. Thus, some of the composite estimates could have less
quality than the numbers indicate. This is true when making estimates of
error for any set of estimates. However, we base our final evaluation of
the quality of the composite estimates when compared to the other
unbiased estimators not on the results for just one estimate, but on the
fact that as a group the estimates of errors for the composite
estimators are almost uniformly better than those for the more standard
design-based estimates.
Table 3. Average and maximum relative mean squared errors (RMSEs) by state size group for typical estimates: Composite estimation using regional estimates
| |
|
Conditional mean
expenditures |
Percent of persons with
expenditure |
Expenditure
Type |
Size
Group |
Mean
RMSE |
Max
RMSE |
Mean
RMSE |
Max
RMSE |
| All types combined |
1 |
0.0587 |
0.0914 |
0.0107 |
0.0189 |
| All types combined |
2 |
0.0533 |
0.1116 |
0.0117 |
0.0176 |
| All types combined |
3 |
0.0758 |
0.1556 |
0.0143 |
0.0241 |
| Dental visits |
1 |
0.0699 |
0.1032 |
0.0418 |
0.0629 |
| Dental visits |
2 |
0.0688 |
0.1311 |
0.0536 |
0.0682 |
| Dental visits |
3 |
0.0912 |
0.1742 |
0.0719 |
0.1378 |
| Inpatient facility |
1 |
0.1086 |
0.1441 |
0.0694 |
0.0989 |
| Inpatient facility |
2 |
0.1217 |
0.1521 |
0.0587 |
0.1149 |
| Inpatient facility |
3 |
0.1750 |
0.3330 |
0.0872 |
0.2130 |
| Office based visits |
1 |
0.0598 |
0.1112 |
0.0163 |
0.0272 |
| Office based visits |
2 |
0.0609 |
0.1009 |
0.0182 |
0.0359 |
| Office based visits |
3 |
0.0657 |
0.1240 |
0.0261 |
0.0538 |
| Outpatient doctors |
1 |
0.0866 |
0.1223 |
0.0747 |
0.1212 |
| Outpatient doctors |
2 |
0.1119 |
0.2355 |
0.1243 |
0.1689 |
| Outpatient doctors |
3 |
0.1639 |
0.4506 |
0.1778 |
0.3118 |
| Prescription drugs |
1 |
0.0497 |
0.0841 |
0.0193 |
0.0252 |
| Prescription drugs |
2 |
0.0536 |
0.1053 |
0.0193 |
0.0459 |
| Prescription drugs |
3 |
0.0747 |
0.2189 |
0.0267 |
0.0513 |
Source:
AHRQ, Household Component of the Medical Expenditure Panel Survey, 2002
One can see from table 3 that this technique provides
several advantages.
- In spite of their biased nature,
estimates have uniformly better estimated relative mean squared errors
than the previous two methods.
- Improvement was greatest where it was
needed most, i.e., in size groups 2 and 3 and inpatient facility and
outpatient doctors.
- Improvements were such that one could
make estimates for all expenditure types for state size groups 1 and
2, the 20 largest states, and have very few estimates with greater
than a 20 percent relative standard error and none with a relative
standard error greater than 30 percent. With the exception of errors
for inpatient facility and outpatient doctors, the vast majority of
the estimates for the 20 largest states have relative errors of less
than 10 percent.
- For all but the least common types of
expenditures, inpatient facility and outpatient doctors, most of the
estimates for the set of the smallest states, size group 3, are
acceptable using a 10 percent relative error as the standard of
acceptance. Few of these estimates for the smallest states have
relative error measures of over 20 percent.
One should note that although estimates of totals are
not evaluated, if one has good estimates of means and proportions, one
can make estimates of totals by multiplying means by total population
estimates from other sources.
Return to Table of Contents
Conclusions and Recommendations
We made two sets of direct state estimates with 2002
MEPS-HC data for the 30 largest states. The first set was produced using
standard nationally post-stratified weights, and the second used weights
post-stratified within each of the largest states. Each set of estimates
included estimates for six types of expenditures and three measures, an
estimate for total expenditures, and estimates for conditional mean
expenditure per person with an expenditure and for the percentage of
persons with an expenditure. After this, estimates for the same six
types of expenditures were made for the mean and the percentage with an
expenditure using a small area technique where strength was borrowed for
state estimates from data for the Census Division. Several patterns of
information surfaced:
- Estimates decreased in quality as the
population size of the state decreased and the number of PSUs
decreased.
- The best estimates in any group were for
the percentage of persons who had expenditures. Estimates of error for
the conditional mean expenditure and total expenditures were
correlated with the percentage of persons who had the expenditure,
i.e., sample size used.
- Overall, the relative errors of the
estimates were best for the small area technique and worst based on
the nationally stratified weights.
- One can make estimates for the 20 largest
states for the more common expenditures with the state post-stratified
weights, and one can generally make improved estimates with the small
area technique for each state for all the expenditure types tested.
The research was very successful and confirms the
feasibility for making state estimates with the MEPS-HC to help inform
health policy decisions at the state level. Given these results, it
seems that estimates could be produced for additional survey variables
at the state level for the 20 largest states. Whenever possible, the
method used should be the small area technique. Efforts should be
focused on items that affect a large enough portion of the population so
that enough sample is available to produce estimates with acceptable
quality. Among the items that might be considered are expenditures for
obese and overweight persons, persons with private health insurance or
persons without health insurance, all subsets that might have a large
enough sample to produce reliable estimates.
Given the simplicity of the process and that development
of state stratified weights and software to produce these estimates have
been completed, additional estimates can and should be produced and
assessed to determine how many state-level estimates can be produced on
a regular basis in the future.
Return to Table of Contents
Acknowledgments
The author would like to thank Trena Ezzati-Rice and
Steve Machlin for their valuable ideas and comments which were used
freely in the production of this work.
Return to Table of Contents
References
Botman SL, Moore TF, Moriarity CL, and Parsons VL.
Design and Estimation for the National Health Interview Survey,
1995?004. National Center for Health Statistics, Vital Health Stat
2(130). 2000.
Census Bureau Web site:
a:
http://www.census.gov/programs-surveys/sipp/methodology/sampling.html
b:
http://www.census.gov/hhes/www/housing/ahs/statedata.html
c:
https://www.census.gov/topics/income-poverty/poverty.html
d:
http://www.census.gov/hhes/www/housing/ahs/ahs01/appendixb.pdf
Cohen SB. Sample Design of the 1997 Medical Expenditure
Panel Survey Household Component. MEPS Methodology Report No 11. AHRQ Pub. No.
01-0001. Rockville, MD: Agency for Healthcare Research and Quality. 2000.
http://www.meps.ahrq.gov/
Cochran WG. Sampling Techniques. New York: John
Wiley and Sons. 1977.
DeNavas-Walt C, Proctor BD, and Mills RJ. Income,
Poverty and Health Insurance Coverage in the United States: 2003.
U.S. Census Bureau, Current Population Reports P60-226. U.S. Government
Printing Office: Washington, DC. 2004.
Ghosh M and Rao JNK. Small area estimation: An
appraisal. Statistical Sciences, Vol. 9, No. 1, 55?3. 1994.
Kaiser Family Foundation. Employer Health Benefit,
Annual Survey. Menlo Park, CA. 2004.
Kostanich DL and Dippo CS. Current Population Survey:
Design and Methodology. Technical Paper 63RV. U.S. Government
Printing Office: Washington, DC. 2002.
Machlin SR, Nixon AJ, and Sommers JP. Health Care
Expenditures and Percentage Uninsured in 10 Large Metropolitan Areas,
2000. Statistical Brief #38. Agency for Healthcare Research and
Quality. Rockville, MD. February 2004.
http://www.meps.ahrq.gov/mepsweb/data_files/publications/st38/stat38.pdf
Machlin SR and Sommers JP. Estimates of Health Care
Expenditures for the 10 Largest States, 2002. Statistical Brief #69.
Agency for Healthcare Research and Quality, Rockville, Md. February 2005.
http://www.meps.ahrq.gov/mepsweb/data_files/publications/st69/stat69.pdf
Medical Expenditure Panel Survey Web site:
http://www.meps.ahrq.gov/mepsweb/data_stats/quick_tables_search.jsp?component=1&subcomponent=0
National Association of State Budget Officers.
State Expenditure Report. Washington, DC. 2003.
National Center for Health Statistics Web site:
http://www.cdc.gov/nchs
Prasad NGN and Rao JNK. The estimation of mean squared
errors of small area estimators. Journal of American Statistical Association,
85: 163-171. 1990.
Wolter KM. Introduction to Variance Estimation.
New York: Springer-Verlag. 1985.
Return to Table of Contents
Return to the MEPS Homepage
Suggested Citation:
Sommers, J. P. Producing State Estimates with the Medical Expenditure Panel Survey,
Household Component. Methodology Report No. 16.
December 2005. Agency for Healthcare Research and Quality, Rockville, Md.
http://www.meps.ahrq.gov
/data_files/publications/mr16/mr16.shtml |
