Methodology Report #21:
An Analysis of the Effects of Post-stratification on Errors for Estimates Using the 2003 Medical Expenditure
Panel Survey Household Component
John P. Sommers, PhD, Agency for Healthcare Research and Quality
Table of Contents
Abstract
The Medical Expenditure Panel Survey (MEPS)
Background: Post-stratification
Household Component of the Medical Expenditure Panel Survey and Post-stratification
Results: Taylor Series Error Estimates
Table A. Average relative standard errors using regional raking and Taylor series, MEPS-HC, 2003
Table B. Average relative standard errors using state raking and Taylor series, MEPS-HC, 2003
Results: Balanced Repeated Replication Error Estimates
Table C. Average relative standard errors using regional raking and balanced repeated replication, MEPS-HC, 2003
Table D. Average relative standard errors using state raking and balanced repeated replication, MEPS-HC, 2003
Conclusions and Recommendations
References
Appendix
Abstract
This report shows the effects of post-stratification of
weights for the Household Component of the 2003 Medical Expenditure Panel Survey,
using various sets of marginal control totals on two types of variance
estimates for a variety of national, regional, and state estimates. The variances
estimation methods are a balanced repeated replication BRR method, which includes
the effects of the raking on the variance, and a Taylor series method,
which does not include the effects of raking. It is shown that although the
estimates decrease using the BRR method when a limited set of selected controls are added
to the raking process, the Taylor series estimates for the same values actually
increase.
The estimates in this report are based on the most
recent data available at the time the report was written. However,
selected elements of MEPS data may be revised on the basis of additional
analyses, which could result in slightly different estimates from those
shown here. Please check the MEPS Web site for the most current file
releases.
Center for Financing, Access, and Cost Trends
Agency for Healthcare Research and Quality
540 Gaither Road
Rockville, MD 20850
http://www.meps.ahrq.gov/
Return to Table of Contents
The Medical Expenditure Panel Survey (MEPS)
Background
The Medical Expenditure Panel Survey (MEPS) is conducted
to provide nationally representative estimates of health care use,
expenditures, sources of payment, and insurance coverage for the U.S.
civilian noninstitutionalized population. MEPS is cosponsored by the
Agency for Healthcare Research and Quality (AHRQ), formerly the Agency
for Health Care Policy and Research, and the National Center for Health
Statistics (NCHS).
MEPS comprises three component surveys: the Household
Component (HC), the Medical Provider Component (MPC), and the Insurance
Component (IC). The HC is the core survey, and it forms the basis for
the MPC sample and part of the IC sample. Together these surveys yield
comprehensive data that provide national estimates of the level and
distribution of health care use and expenditures, support health
services research, and can be used to assess health care policy
implications.
MEPS is the third in a series of national probability
surveys conducted by AHRQ on the financing and use of medical care in
the United States. The National Medical Care Expenditure Survey (NMCES)
was conducted in 1977, the National Medical Expenditure Survey (NMES) in
1987. Beginning in 1996, MEPS continues this series with design
enhancements and efficiencies that provide a more current data resource
to capture the changing dynamics of the health care delivery and
insurance system.
The design efficiencies incorporated into MEPS are in
accordance with the Department of Health and Human Services (DHHS)
Survey Integration Plan of June 1995, which focused on consolidating
DHHS surveys, achieving cost efficiencies, reducing respondent burden,
and enhancing analytical capacities. To accommodate these goals, new
MEPS design features include linkage with the National Health Interview
Survey (NHIS), from which the sample for the MEPS-HC is drawn, and
enhanced longitudinal data collection for core survey components. The
MEPS-HC augments NHIS by selecting a sample of NHIS respondents,
collecting additional data on their health care expenditures, and
linking these data with additional information collected from the
respondents’ medical providers, employers, and insurance providers.
Household Component
The MEPS-HC, a nationally representative survey of the
U.S. civilian noninstitutionalized population, collects medical
expenditure data at both the person and household levels. The HC
collects detailed data on demographic characteristics, health
conditions, health status, use of medical care services, charges and
payments, access to care, satisfaction with care, health insurance
coverage, income, and employment.
The HC uses an overlapping panel design in which data
are collected through a preliminary contact followed by a series of five
rounds of interviews over a two and a half year period. Using
computer-assisted personal interviewing (CAPI) technology, data on
medical expenditures and use for two calendar years are collected from
each household. This series of data collection rounds is launched each
subsequent year on a new sample of households to provide overlapping
panels of survey data and, when combined with other ongoing panels, will
provide continuous and current estimates of health care expenditures.
The sampling frame for the MEPS-HC is drawn from
respondents to NHIS, conducted by NCHS. NHIS provides a nationally
representative sample of the U.S. civilian noninstitutionalized
population, with oversampling of Hispanics and blacks.
Medical Provider Component
The MEPS-MPC supplements and validates information on
medical care events reported in the MEPS-HC by contacting medical
providers and pharmacies identified by household respondents. The MPC
sample includes all hospitals, hospital physicians, home health
agencies, and pharmacies reported in the HC. Also included in the MPC
are all office-based physicians:
- Providing care for HC respondents receiving Medicaid.
- Associated with a 75 percent sample of households
receiving care through an HMO (health maintenance organization) or managed
care plan.
- Associated with a 25 percent sample of the remaining
households. Data are collected on medical and financial characteristics of
medical and pharmacy events reported by HC respondents, including:
- Diagnoses coded according to ICD-9 (9th Revision,
International Classification of Diseases) and DSMIV (Fourth Edition,
Diagnostic and Statistical Manual of Mental Disorders).
- Physician procedure codes classified by CPT-4
(Current Procedural Terminology, Version 4).
- Inpatient stay codes classified by DRG (diagnosis
related group).
- Prescriptions coded by national drug code (NDC),
medication names, strength, and quantity dispensed.
- Charges, payments, and the reasons for any
difference between charges and payments.
The MPC is conducted through telephone interviews and
mailed survey materials.
Insurance Component
The MEPS-IC collects data on health insurance plans
obtained through private and public sector employers. Data obtained in
the IC include the number and types of private insurance plans offered,
benefits associated with these plans, premiums, contributions by
employers and employees, and employer characteristics.
Establishments participating in the MEPS-IC are selected
through three sampling frames:
- A list of employers or other insurance providers identified
by MEPS-HC respondents who report having private health insurance at the Round 1
interview.
- A Bureau of the Census list frame of private-sector business
establishments.
- The Census of Governments from the Bureau of the Census.
To provide an integrated picture of health insurance,
data collected from the first sampling frame (employers and other
insurance providers) are linked back to data provided by the MEPS-HC
respondents. Data from the other three sampling frames are collected to
provide annual national and state estimates of the supply of private
health insurance available to American workers and to evaluate policy
issues pertaining to health insurance. Since 2000, the Bureau of Economic
Analysis has used national estimates of employer contributions to group
health insurance from the MEPS-IC in the computation of Gross Domestic
Product (GDP).
The MEPS-IC is an annual panel survey. Data are
collected from the selected organizations through a prescreening
telephone interview, a mailed questionnaire, and a telephone follow-up
for nonrespondents.
Survey Management
MEPS data are collected under the authority of the
Public Health Service Act. They are edited and published in accordance
with the confidentiality provisions of this act and the Privacy Act.
NCHS provides consultation and technical assistance.
As soon as data collection and editing are completed,
the MEPS survey data are released to the public in staged releases of
summary reports and microdata files. Summary reports are released as
printed documents and electronic files. Microdata files are released on
CD-ROM and/or as electronic files.
Printed documents and CD-ROMs are available through the
AHRQ Publications Clearinghouse. Write or call:
AHRQ Publications Clearinghouse
Attn: (publication number)
P.O. Box 8547 Silver Spring, MD 20907
800-358-9295
703-437-2078 (callers outside the United States only)
888-586-6340 (toll-free TDD service; hearing impaired only)
To order online, send an e-mail to: ahrqpubs@ahrq.gov.
Be sure to specify the AHRQ number of the document or
CD-ROM you are requesting. Selected electronic files are available
through the Internet on the MEPS Web site:
http://www.meps.ahrq.gov/
For more information, visit the MEPS Web site or e-mail
mepspd@ahrq.gov.
Return to Table of Contents
Background: Post-stratification
Post-stratification is a process used in survey sampling
in which estimates from a survey are normalized to external control
totals by adjusting the weights of the sampling units so that they add
to external totals. These totals are usually Census or other values that
are considered to have no error or far less error than the estimates
from the survey. Although weight adjustments can be quite complex, a
simple example of the most straightforward method, cell adjustment,
where adjustment is done by adjusting the weights for a set of cell as
follows:
Suppose we had a demographic person-level survey where
each person had a weight
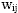where i = 1 or 2 and j = 1, 2...
 .
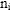Suppose that the value of i indicated the gender of the respondent and
for some measurement,
 ,
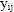collected from each person, the gender of the person was highly
correlated with the value of
.
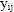An example would be the height of the respondent.
Suppose one desired an estimate of the average height of
the entire population. Using only information from the survey, then the
estimate of average height would be
a simple average.
However, if
were the census total for the ith group, then a better estimate might be
 ,
where
If one defined
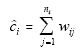
then one could see that
 .
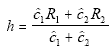Thus, one has basically formed the new estimate,
 ,
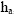by replacing estimates of the number in each group with a better
estimate or census total. If the expected values of the R’s for each
group are very different and the estimation errors for the R’s are not
large this new estimate could be much better than the original estimate
for the average.
One can see that if one changed the weights to
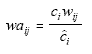
then if these adjusted weights were used in the original
estimate the adjusted estimate would be obtained. Thus, one can use the
old form of the estimator and the adjusted weights to obtain the new
adjusted estimates.
In general, simple cell adjustment post-stratification
could break the population into many more cells. These cells could be
defined by the crosses of several variables. At this point, the estimate
for the entire data set would be
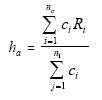
In the cell adjustment method just specified, because
adjustments to the weights are the same for each person in the cell, the
estimates
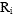are the original estimates for the average for the cell. This is not always
the case with weight-adjustment methods.
Return to Table of Contents
If the cells were defined using the cross of more than
one cell-defining variable, then the adjustment is made for cells
defined using the cross of all the variables. For instance, if one had
two gender groups and five age groups, there would be 10 cells and each
cell would have its population adjusted to the population total, and the
R’s would be the estimates using the original weights for the rate for
the persons with both characteristics used to define the cell, persons
of both a specific gender and age group.
There is improvement in precision if the expected values
of the R’s are dispersed and the sampling errors in the R’s are not as
large relative to the differences in expected values. If the errors are
larger than the differences, the errors essentially mask the difference
in expected values. For example, if the expected R’s were equal in value
and their errors were large because cell samples were small,
post-stratification would not help because there is no difference in the
cell average, so they should be combined to make a better estimate of
the single R value. In such cases, there could be higher precision if
the number of cells were reduced. Kish says this happens when the
samples in the sub cells are subject to variability and the
sample sizes become significantly out of proportion to the cell totals
(Kish, 1965).
The effects of post-stratification on standard errors
depend upon the survey and the cells. However, its positive effects may
be minimal. According to Kish, it seldom results in large gains, and
Korn and Graubard (1999) imply it has little effect and that most people
do not consider post-stratification in their error calculations because
the difference in results would be minimal. Kish also notes that the
counts being estimated from the survey must be the same item as the
control total being used or there is bias in the values of the
post-stratified estimate. Thus, for instance, if the control counts came
from another survey that had a different expected value in its counts
per cell due to question differences or different methods of
administration of the surveys, bias could occur if counts with different
expected values per cell from the other survey were used for
post-stratification. One should also note that the adjustment of weights
may increase the variability of the weights and lead to higher errors
for domains that are not one of the weighting cells.
Another common method of using control totals is raking.
In this method, the sum of the weights, the estimate of the population
for the cell, is again adjusted to population totals. However, if
multiple variables are used in raking, the weights are adjusted so that
the marginal totals are equal to the population totals, not the values
for the individual cells made by crossing the variables. Thus, in our
example above with two gender and five age classes, the sample totals
would equal the population totals for the two gender groups and five age
groups but not the cell defined by the cross of each a specific gender
and age group. This type of adjustment is usually done using some type
of iterative process.(Kalton and Flores-Cervantes, 2003.)
When raking is used, the values of the R’s for the raked
cells are not the original R values because weights are changed within
the cells. Thus, if, for example, we raked over two dimensions, age and
race, then if we considered the sum over age:
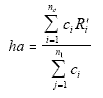
we would need to consider the effect of changed weights
on the variance of
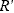because the raking can change the weights within the cells when
raking is done. One needs to be cautious, as this unequal weighting may
increase the error more than the controlling of the weights to
population can decrease it.
Typically, post-stratification cells are defined using
age, race/ethnicity, and sex plus perhaps a variable that is uniquely
related to the purpose of the survey. For instance, the National Survey
of Family Growth uses number of children born along with the standard
demographics. Cell classification is likely to be used if sample sizes
within cells support this method. However, if not, then raking might be
used to cut the numbers of cells.(Korn and Graubard, 1999)
Return to Table of Contents
Household Component of the Medical Expenditure Panel Survey and
Post-stratification
The Household Component of the Medical Expenditure Panel
Survey (MEPS-HC) is a national household survey of the U.S. civilian
noninstitutionalized population. The survey collects information on the
respondent’s health, health care, and health expenditures along with
certain personal demographic, insurance, and job information. Currently,
the sample for the HC is selected as a subsample of respondents from the
National Health Interview Survey (NHIS) (Cohen, 2000). The sample
contains an over sample of blacks, Hispanics, Asians, and poor (MEPS Web
site). The final weights are for the HC are created using adjustments to
the NHIS weights. The weights are adjusted for dwelling unit nonresponse,
person-level (survey attrition) nonresponse. After nonresponse
adjustment, the weights are adjusted using a complex raking
poststratification adjustment that uses multiple sets of controls
developed using sets of cells defined using crosses of age,
race/ethnicity, sex, region, poverty status, and metropolitan
statistical area (MSA) status (whether one lives in an MSA)
(Alvarez-Rojas, 2005). The purpose of this analysis is to gain knowledge
of the effects of raking post-stratification on MEPS-HC error estimates.
To begin this analysis, we created a large number of
sets of post-stratified weights for the MEPS-HC 2003 data. These weights
were created by raking to an array of control totals defined by the
factors region, state, race/ethnicity, age, MSA status, poverty status,
and gender. Basically, we created a set of weights within region that
were raked to each of the other factors except state and gender,
individually, then using these four marginals raked to each combination
of two marginals, then combinations of three marginals, and four
marginals. We then did the case with five marginals by including the
gendermarginal control. The list of different sets of marginals
considered can be seen more clearly in the next sections, which discuss
results. We did not do any weights where the controls were defined by
the cross of two of the controls within region. So, when we say we raked
to the region, by age and MSA status, we mean we raked to the age and
MSA status marginals within each of the four regions. We repeated the
process by using a set of state-defined geographic cells where each of
the 30 largest states was an individual cell similar to a region, and
the remaining states within each region made up four more cells. Thus,
if we say we raked to state by age and MSA status, it means we raked to
the state marginal totals for age group and MSA status group within each
of the 34 state groups. This created a much finer break. We did only the
30 states individually because from experience we knew that for the
remaining states the samples were very small andestimates could not be
made for the smallest states. The definitions of cells that define the
marginals can be seen in the Appendix. We also created national,
regional, and state post-stratifications by using the geographic
controls to do a cell adjustment for each of the three sets of
geographic cells. These were done as base cases. Note: We did not trim
the weights as is done in the actual raking with the MEPS-HC, since in
2003 only one weight was trimmed and our largest weights after raking
were not much different than those in operations after trimming. Thus,
we believed for this project trimming was not necessary.
With each set of weights, we created a set of national-,
regional-, and state-level estimates for six types of expenditure
classes: all, dental, prescription drugs, office based, hospital
outpatient, and hospital inpatient. For each class, we created estimates
of the percentage of persons with an expenditure, the mean expenditure
for those with an expenditure, the percentage paid out of pocket, and
the percentage paid by private insurance. For each estimate, we created
a variance estimate using two methods:
- Taylor series method, which does not consider the
effect of post-stratification of errors.
- Balanced repeated replication (BRR), where the sets
of weights were raked for each of the replicates to the control totals. This
method should show effects of the post-stratification on the error estimates.
(Wolter, 1985)
Since the MEPS-HC sample that is post-stratified to the
set of point-in-time control totals is the set of persons in the sample
who are still living at the end of the survey year, this sample was the
only sample used in this study. This sample is the vast majority of the
total MEPS-HC sample, and the relative results should still hold when
the small amount of other sample is included in estimates. This dropped
sample includes a small number of persons in the total sample who die
during the year or who are in the civilian noninstitutionalized
population for only part of the year. This small sample does not go
through the post-stratification process we are discussing. (MEPS Web
site)
Return to Table of Contents
Results: Taylor Series Error Estimates
The results of Taylor Series estimation of relative
standard errors (RSE) using the various sets of raked weights are given
in tables A and B. Table A has the results for estimates made with
weights raked at the regional level, and table B has results where the
raking cells were created at the state level. For each sets of raked
weights, there are 4 averages given. The first is for 120 estimates of
means made at the national and regional levels. The second set is for
the 816 mean estimates at the state level. The third set is for
estimates of sums made at the national and regional levels. The fourth
set is for estimates of sums made at the state level. We divided the
results into these categories because these groupings show the key
differences in results. In reviewing these results, one must remember
that the Taylor Series estimates of error do not reflect the effects of
post-stratification.
The following are some key features of these results:
- There is not a wide range of results for any of the
types of estimates.
- For means for each set of estimates (column), the
average errors are higher for post-stratification to the same defining variables
done at the state than the regional level. (For example, the results for means
for the weights raked to poverty at state level are higher than those for weights
raked to poverty at the regional level.)
- For means for each set of estimates, there is a high
correlation between the standard errors of the distributions of the sets of
weights and the average standard errors obtained with the set of weights. This
is true for each of the two mean columns taken individually in table A or table B.
It is also true for each of the two columns if the results from tables A and B
are pooled. Since the state post-stratifications in table B have many more sets
of controls, this would imply the fact reported in the second feature above.
Table A. Average relative standard errors using regional raking and Taylor series, MEPS-HC, 2003
| |
|
Average relative standard errors |
| |
|
Mean estimates |
Sum estimates |
| Regional raking cells |
Std error of weights |
Regional/national estimates |
State estimates |
Regional/national estimates |
State estimates |
| National* |
6001 |
0.05523 |
0.13637 |
0.08981 |
0.32013 |
| None** |
6012 |
0.05524 |
0.13637 |
0.08980 |
0.32013 |
| Age |
6092 |
0.05581 |
0.13672 |
0.09015 |
0.32018 |
| Ethnicity |
6006 |
0.05529 |
0.13639 |
0.08990 |
0.32015 |
| MSA |
5958 |
0.05462 |
0.13604 |
0.08927 |
0.31809 |
| Poverty |
6069 |
0.05529 |
0.13629 |
0.09007 |
0.32035 |
| Age, Ethnicity |
6075 |
0.05584 |
0.13674 |
0.09021 |
0.32019 |
| Age, MSA |
6040 |
0.05513 |
0.13638 |
0.08960 |
0.31818 |
| Age, Poverty |
6145 |
0.05587 |
0.13672 |
0.09036 |
0.32037 |
| Ethnicity, MSA |
5922 |
0.05461 |
0.13606 |
0.08924 |
0.31798 |
| Poverty, Ethnicity |
6049 |
0.05528 |
0.13627 |
0.09003 |
0.32035 |
| Poverty, MSA |
6037 |
0.05463 |
0.13587 |
0.08953 |
0.31840 |
| Age, Ethnicity, MSA |
5994 |
0.05506 |
0.13643 |
0.09009 |
0.32001 |
| Age, Poverty , Ethnicity |
6112 |
0.05586 |
0.13672 |
0.09030 |
0.32036 |
| Age, Poverty, MSA |
6107 |
0.05514 |
0.13632 |
0.08980 |
0.31844 |
| Age, Ethnicity, Sex |
6078 |
0.05589 |
0.13678 |
0.09025 |
0.32024 |
| Poverty, Ethnicity, MSA |
5983 |
0.05453 |
0.13582 |
0.08936 |
0.31823 |
| Age, Poverty , Ethnicity, MSA |
6051 |
0.05505 |
0.13630 |
0.08961 |
0.31827 |
| Age, Poverty , Ethnicity, MSA, Sex |
6052 |
0.05506 |
0.13631 |
0.08961 |
0.31831 |
*
Raked to national total only
**
Raked to regional totals only, no sub-regional raking
Return to Table of Contents
Table B. Average relative standard errors using state raking and Taylor series, MEPS-HC, 2003
| |
|
Average relative standard errors |
| |
|
Mean estimates |
Sum estimates |
| State raking cells |
Std error of weights |
Regional/national estimates |
State estimates |
Regional/national estimates |
State estimates |
| National* |
6001 |
0.05523 |
0.13637 |
0.08981 |
0.32013 |
| None** |
6210 |
0.05624 |
0.13637 |
0.08844 |
0.32013 |
| Age |
6334 |
0.05660 |
0.13735 |
0.08831 |
0.31971 |
| Ethnicity |
6317 |
0.05632 |
0.13603 |
0.08862 |
0.32016 |
| MSA |
6368 |
0.05624 |
0.13771 |
0.0887 |
0.31943 |
| Poverty |
6404 |
0.05681 |
0.13760 |
0.08884 |
0.32065 |
| Age, Ethnicity |
6435 |
0.05660 |
0.13689 |
0.08843 |
0.31971 |
| Age, MSA |
6485 |
0.05658 |
0.13865 |
0.08867 |
0.31924 |
| Age, Poverty |
6522 |
0.05697 |
0.13867 |
0.08849 |
0.32019 |
| Ethnicity, MSA |
6474 |
0.05637 |
0.13734 |
0.08906 |
0.31969 |
| Poverty, Ethnicity |
6482 |
0.05673 |
0.13706 |
0.08887 |
0.32072 |
| Poverty, MSA |
6565 |
0.05661 |
0.13854 |
0.08890 |
0.32002 |
| Age, Ethnicity, MSA |
6585 |
0.05634 |
0.13809 |
0.08901 |
0.32124 |
| Age, Poverty , Ethnicity |
6600 |
0.05677 |
0.13803 |
0.08839 |
0.32025 |
| Age, Poverty, MSA |
6673 |
0.05674 |
0.13958 |
0.08860 |
0.31969 |
| Age, Ethnicity, Sex |
6445 |
0.05660 |
0.13697 |
0.08842 |
0.31968 |
| Poverty, Ethnicity, MSA |
6643 |
0.05663 |
0.13795 |
0.08918 |
0.32029 |
| Age, Poverty , Ethnicity, MSA |
6752 |
0.05665 |
0.13898 |
0.08871 |
0.31995 |
| Age, Poverty , Ethnicity, MSA, Sex |
6760 |
0.05662 |
0.13911 |
0.08865 |
0.31989 |
*
Raked to national total only
**
Raked to state totals only, no sub-state raking
Return to Table of Contents
Results:
Balanced Repeated Replication Error Estimates
The BRR results are shown in tables C and D. Table C
contains results of average RSE’s for regional post-stratifications and
table D state-level post-stratifications. The BRR results have estimates
that are at overall levels similar to those of the Taylor Series.
However, the patterns and relationships among the results are different
since these results reflect the effect of post-stratification on the
variances.
Some of the key results from the BRR results include the
following:
- Post-stratification has a small but significant effect on the errors of
the estimates. For instance, for regional and national estimates and
regional post-stratification, the best results for means decline about 4
percent relative to the estimates with simple one-cell national-level
post-stratification.
- Adding raking variables generally improves results. Results with two variables
are generally better than those with one variable, three variables
better than two, etc. Adding the fifth variable, sex, only seems to help
for totals. However, this may be because sex is a weak predictor, not
because we have reached any limit caused by using too many cells.
- Of the four main variables used, age, ethnicity, MSA status, and poverty, there
seems to be no clear pattern of variables that consistently gives better
results in terms of precision. For instance, for regional-level means,
the variable that singly gave the best improvement when raking to region
crossed with that variable, poverty seems to be the single most
important variable. But for the state-level estimates with state raking,
age seems to be the single most important variable. It may be that
because improvements in results are so small, although all the variables
improve results, as seen with the overall downward trend when more
variables are added, that it is impossible to order the variables in
their overall effect.
- Regional raking works best for regional results and state raking works best for
state results. State-level raking for regional and national estimates
may create too many cells for those types of estimates.
- Any type of geographic raking to a geographic level equal or below that of the
estimates has a marked effect on the errors of totals. State or regional
raking helped regional estimates for totals significantly. State-level
raking improved state estimates, but regional raking did not.
- There was no significant correlation within groups of estimates with the
standard errors of the estimates.
Table C. Average relative standard errors using regional raking and balanced repeated replication, MEPS
| |
|
Average relative standard errors |
| |
|
Mean estimates |
Sum estimates |
| Regional raking cells |
Std error of weights |
Regional/national estimates |
State estimates |
Regional/national estimates |
State estimates |
| National* |
6001 |
0.05505 |
0.14061 |
.09431 |
.31878 |
| None** |
6012 |
0.05504 |
0.14061 |
.06794 |
.31265 |
| Age |
6092 |
0.05452 |
0.14044 |
.06675 |
.31175 |
| Ethnicity |
6006 |
0.05481 |
0.14065 |
.06870 |
.31156 |
| MSA |
5958 |
0.05431 |
0.14027 |
.06748 |
.31042 |
| Poverty |
6069 |
0.05428 |
0.14063 |
.06712 |
.31238 |
| Age, Ethnicity |
6075 |
0.05424 |
0.14046 |
.06629 |
.31067 |
| Age, MSA |
6040 |
0.05379 |
0.14011 |
.06610 |
.30959 |
| Age, Poverty |
6145 |
0.05393 |
0.14030 |
.06614 |
.31145 |
| Ethnicity, MSA |
5922 |
0.05402 |
0.14027 |
.06666 |
.30908 |
| Poverty, Ethnicity |
6049 |
0.05422 |
0.14038 |
.06706 |
.31141 |
| Poverty, MSA |
6037 |
0.05349 |
0.13990 |
.06628 |
.31025 |
| Age, Ethnicity, MSA |
5994 |
0.05342 |
0.14035 |
.06598 |
.31018 |
| Age, Poverty , Ethnicity |
6112 |
0.05383 |
0.14075 |
.06598 |
.31049 |
| Age, Poverty, MSA |
6107 |
0.05315 |
0.13992 |
.06544 |
.30939 |
| Age, Ethnicity, Sex |
6078 |
0.05429 |
0.14053 |
.06623 |
.31078 |
| Poverty, Ethnicity, MSA |
5983 |
0.05333 |
0.13991 |
.06616 |
.30903 |
| Age, Poverty , Ethnicity, MSA |
6051 |
0.05298 |
0.13996 |
.06522 |
.30820 |
| Age, Poverty , Ethnicity, MSA, Sex |
6052 |
0.05302 |
0.14001 |
.06513 |
.30830 |
*
Raked to national total only
**
Raked to regional totals only, no sub-regional raking
Return to Table of Contents
Table D. Average relative standard errors using state raking and balanced repeated replication, MEPS-HC, 2003
| |
|
Average relative standard errors |
| |
|
Mean estimates |
Sum estimates |
| State raking cells |
Std error of weights |
Regional/national estimates |
State estimates |
Regional/national estimates |
State estimates |
| National* |
6001 |
.05505 |
.14061 |
.09431 |
.31878 |
| None** |
6210 |
.05632 |
.14061 |
.06868 |
.18075 |
| Age |
6334 |
.05596 |
.13746 |
.06777 |
.17516 |
| Ethnicity |
6317 |
.05626 |
.13981 |
.06870 |
.18032 |
| MSA |
6368 |
.05555 |
.13948 |
.06731 |
.17889 |
| Poverty |
6407 |
.05637 |
.14063 |
.06877 |
.18068 |
| Age, Ethnicity |
6435 |
.05585 |
.13664 |
.06629 |
.17473 |
| Age, MSA |
6485 |
.05512 |
.13621 |
.06669 |
.17325 |
| Age, Poverty |
6525 |
.05574 |
.13763 |
.06725 |
.17490 |
| Ethnicity, MSA |
6473 |
.05551 |
.13861 |
.06748 |
.17824 |
| Poverty, Ethnicity |
6484 |
.05611 |
.13950 |
.06853 |
.18021 |
| Poverty, MSA |
6568 |
.05544 |
.13902 |
.06736 |
.17833 |
| Age, Ethnicity, MSA |
6585 |
.05476 |
.13519 |
.06671 |
.17392 |
| Age, Poverty , Ethnicity |
6602 |
.05540 |
.13643 |
.06693 |
.17459 |
| Age, Poverty, MSA |
6677 |
.05477 |
.13582 |
.06612 |
.17250 |
| Age, Ethnicity, Sex |
6444 |
.05583 |
.13658 |
.06749 |
.17459 |
| Poverty, Ethnicity, MSA |
6646 |
.05527 |
.13787 |
.06737 |
.17788 |
| Age, Poverty , Ethnicity, MSA |
6585 |
.05455 |
.13465 |
.06604 |
.17224 |
| Age, Poverty , Ethnicity, MSA, Sex |
6762 |
.05453 |
.13473 |
.06590 |
.17218 |
*
Raked to national total only
**
Raked to state totals only, no sub-state raking
Return to Table of Contents
Conclusions and Recommendations
From this current research performed until now on
post-stratification of MEPS-HC data, we see that:
-
Post-stratification with the key non-geographic HC variables for the
most part has improved results. No one variable seems to be the most
effective over all types of estimates..
- Post-stratification
by state is useful for state estimates, especially totals, but not
higher-level geographic estimates.
- It appears that
the use of all the five raking dimensions selected does not cause the
quality of results to diminish when done at the regional level. This
would indicate that more post-stratification dimensions could possibly
be added at the regional level without decreasing the quality of the
results.
- Taylor Series
estimates of error are of the same magnitude as the BRR estimates that
take into account the effects of post-stratification. However, they
increase slightly as the weights are post-stratified, even for
post-stratification that actually improves the actual expected error
indicated with BRR error estimates that consider the effects of
post-stratification.
It is recommended that:
- State estimates be
made with data that is post-stratified to state control totals plus at
least age and ethnicity.
- More work be done
with post-stratification at the regional level using somewhat more
complex marginal control totals. For instance, one might want to add
cross classifications of some the variables for the regional marginal
controls; e.g., one might use age crossed with ethnicity or MSA status
control totals.
- Other variables be
tried in the raking that are not now used in the HC raking. An example
would be marital status.
- The effect of
post-stratification at the national level using more complex sets of
cells, such as cells defined by crosses of three variables, be examined
for nationaland regional-level estimates.
- The effect of the
current HC post-stratification be evaluated.
Return to Table of Contents
References
Alvarez-Rojas, L. (2005). Panel 7 and Panel 8
combined, Full Year 2003: raking person weights including the poverty status to obtain the
Expenditure person weights. Memorandum to Tom Hankins. Internal Memorandum, WGTS
1230.02, D-P7P8FY03: 10.02, Rockville, Md.: Westat, Inc.
Cohen, S. B. Sample Design of the 1997
Medical Expenditure Panel Survey Household Component. MEPS Methodology Report No. 11 AHRQ
Pub No. 01-0001. AHRQ: Rockville, Md.: 2000.
Kalton, G. and Flores-Cervantes, I. (2003).
Weighting Methods. Journal of Official Statistics, 19, 81-97.
Kish, L. Survey Sampling. New
York: Wiley: 1965.
Korn, E. L. and Graubard, B. I. Analysis of Health Surveys.
New York: Wiley: 1999.
MEPS Web site. HC-082 2004 Full Year Population
Characteristics File (replaced by HC-089 Full Year Consolidated Data File).
http://www.meps.ahrq.gov/mepsweb/data_stats/download_data_files_detail.jsp?cboPufNumber=HC-089
Wolter, K. M. Introduction to Variance
Estimation. New York: Springer-Verlag: 1985.
Return to Table of Contents
Appendix
Variable Sex
Male
Female
Variable MSA
non-MSA
MSA
Variable Region
Northeast
Midwest
South
West
Variable Poverty
Poor/near poor (less than 125 percent of poverty line)
Low (125 percent to 200 percent of poverty line)
Middle (200 percent to 400 percent of poverty line)
High (over 400 percent of poverty line)
Variable Ethnicity
Hispanic
Non-Hispanic black
Others
Variable Age
0
1-19
20-29
30-44
45-64
65 and over
Return to Table of Contents
Return to the MEPS Homepage
Suggested Citation:
Sommers, J. P. An Analysis of the Effects of Post-stratification on Errors for
Estimates Using the 2003 Medical Expenditure Panel Survey Household Components. Methodology
Report No. 21. March 2007. Agency for Healthcare Research and Quality, Rockville, Md. http://www.meps.ahrq.gov/mepsweb/data_files/publications/mr21/mr21.shtml |
Back
Email Updates