Methodology Report #10: Imputation of Employer Information for the 1996 MEPS Insurance Component
by John Paul Sommers, Ph.D., Agency for Healthcare Research and Quality
Select for more information on
Health Care Information and Electronic Ordering Through the AHRQ Web Site.
Abstract
The Medical Expenditure Panel Survey (MEPS) is the third in a series of nationally representative surveys of medical care use and expenditures sponsored by the Agency for Healthcare Research and Quality (AHRQ). MEPS comprises four component surveys. The Insurance Component (IC) is a survey of employers, unions, and other providers of health insurance. The IC has two parts. The household sample is linked to sample persons in the MEPS Household Component. It consists of private- and public-sector employers of MEPS respondents, as well as unions and insurance companies that provide insurance to the respondents. The list sample consists of an independent random sample of private-sector business establishments, governments, and the self-employed with no employees. This report describes the process used to impute values for missing establishment and plan characteristics for the IC in four types of cases: list sample, private sector; list sample, government; household sample, private sector; and household sample, government. The description includes preparation of the data, selection of donors, and the use of donor and other information to create the item for the recipient.
Select for information on The Medical Expenditure Panel Survey (MEPS).
Introduction
The 1996 Medical Expenditure Panel Survey (MEPS) Insurance Component (IC) is a survey of employers, the self-employed with no employees (SENEs), unions, and insurance companies. The survey is sponsored by the Agency for Healthcare Research and Quality and conducted by the U.S. Bureau of the Census. It is designed to collect employment-related health insurance information, such as premiums and types of plans offered. Information on respondent characteristics, such as size of business, employee characteristics, and industry, is also collected. The 1996 MEPS IC was first administered in 1997; data were collected for the entire 1996 calendar year. Hence, 1996 refers to the data year, not the time of collection.
The sample has two parts:
- The household sample, which is linked to members of the household sample from the MEPS Household Component (HC). It consists of private- and public-sector employers of MEPS respondents, as well as unions and insurance companies that provide them insurance.
- The list sample, which consists of an independent random sample of private-sector business establishments, governments, and SENEs. (An establishment is a single business location, as opposed to a firm, which is a legal entity that can be made up of multiple establishments.)
Return To Top
The IC household sample is defined by the sample design of the MEPS HC (Cohen, 1997) and has persons as sample units. Data are collected from the employers and other insurance providers of the household respondents from the HC. The employers and other providers are proxy respondents for supplemental information on health insurance offered to the household respondent through the employer or other insurance provider. Hence, the probabilities of selection and the corresponding weights for these employers are the same as those of the household sample members and come from the HC design. The data collected in the IC household sample are combined with other information collected directly from household sample cases, and the two types of data can be analyzed together. For instance, with the use data collected in the HC and the description of coverage in the IC, a person's use of health care can be analyzed relative to the types of health insurance coverage he or she has.
The IC list sample is a random sample of establishments selected only for the IC. Its selection is independent of the HC design (Sommers, 1999). The two IC samples (household and list) are combined for collection purposes. The data collected for both samples are very similar for most cases. To understand the imputation process described in this report, it is essential to understand the type of information collected for each type of case, outlined below.
Return To Top
- List sample, private sector-Information on establishment characteristics, whether insurance is offered, and characteristics of plans offered.
- List sample, government-Information on government characteristics, whether insurance is offered, and characteristics of plans offered.
- Household sample, private sector-Information on establishment characteristics, whether insurance is offered, and characteristics of plans offered, plus a small amount of information concerning the plan selected by the household respondent.
- Household sample, government-Information on government characteristics, whether insurance is offered, and characteristics of plans offered, plus a small amount of information concerning the plan selected by the household respondent.
- SENE-Information concerning the self-employed person's health plan, if any, and some personal demographics.
- List sample, private sector-Information on establishment characteristics, whether insurance is offered, and characteristics of plans offered.
- List sample, government-Information on government characteristics, whether insurance is offered, and characteristics of plans offered.
- Household sample, private sector-Information on establishment characteristics, whether insurance is offered, and characteristics of plans offered, plus a small amount of information concerning the plan selected by the household respondent
- .Household sample, government-Information on government characteristics, whether insurance is offered, and characteristics of plans offered, plus a small amount of information concerning the plan selected by the household respondent.
- SENE-Information concerning the self-employed person's health plan, if any, and some personal demographics.
- Household sample, union-Characteristics of the union, characteristics of plans offered, and which plan the household respondent selected.
- Household sample, insurance company-Plan characteristics of insurance selected by household respondent.
Very similar information is collected for the following cases:
- List sample, private sector.List sample, government.Household sample, private sector.
- Household sample, government.
Return To Top
A core set of employer information, such as total employment, selected characteristics, and health coverage offered, is collected for all four of these samples. For the two household samples there are a few additional questions about the household respondent.
As with other surveys, individual respondents in the MEPS IC may not answer all the questions presented. As is the custom for most surveys, important items that are missing are completed for all respondents using a process called imputation. This provides the same full set of critical items for each respondent to anyone who wants to perform analyses with the data.
In the case of the MEPS IC, the core of the imputation process is a form of "hot-deck" imputation, by which information for missing items is derived for an individual respondent using information from a similar respondent that has provided the necessary information. The respondent receiving information is called the recipient and the respondent providing information is called the donor. (See Cox and Cohen, 1985, and Kalton and Kasprzyk, 1986.)
This report describes the process used to impute values for missing establishment and plan characteristics for the survey in four types of cases (list sample, private sector; list sample, government; household sample, private sector; and household sample, government) when the respondent returned enough information to be considered usable but did not complete all the questions on the survey form. The description includes preparation of the data, selection of donors, and the use of donor and other information to create the item for the recipient.
The process used for all the private-sector cases for these data items is the same whether the case came from the household or list sample. Likewise, the process used for the data for all government cases is the same. Furthermore, government and private-sector imputation differ only in the selection of the donors to provide information for missing data. Government cases that require imputation receive information only from other government cases. Private-sector cases receive information only from other private-sector cases. Because of these similarities, the description of the methodology focuses on the imputation of information for private-sector cases. The question numbers refer to questions on Form MEPS-10, which is shown as Appendix A. After the private-sector process is described, differences in the process for the public-sector data are noted.
The questions listed in this report were considered the critical items for the MEPS IC. They were the only items imputed for survey year 1996.
Return To Top
The entire process includes more than merely selecting donor values to replace missing values. Many steps are required to create data that are both consistent and logical.
To impute the data for the MEPS IC, the set of items to be imputed was divided into groups. Items within each group are usually related. Groups are composed of either similar types of items or items that require internal consistency and thus must be imputed and edited together. For instance, the first group of items imputed includes numbers of total and part-time employees eligible for insurance and those who are enrolled. Because of size relations among the variables, they were imputed as part of the same process to assure that the values met consistency criteria (e.g., the total number of eligible employees cannot be less than the number enrolled).
The groups of items were also ordered. This is the order of the actual imputation process, chosen to assure overall consistency and correlation within the data records. For instance, if a particular variable was a primary determinant of the value of another variable, it had to be imputed first. Size of premium is an example. The premiums vary by the type of providers that are available to the insured. Can the insured use only a selected group of providers, or can the insured use any provider but some are preferred by the insurance company, or does the plan pay equally for any and all providers? Thus, before premiums were imputed, type of providers for the plan was imputed. Then the imputed value of the type of providers was used to impute the plan premium, if necessary. This helps retain the relationship between the two variables.
Three steps were usually used to impute items within each group:
- Data preparation--In this step, the data were readied, including such processes as logical edits to fill in results, determination of the set of cases that required imputation for the group of items, and normalization of items to the same basis, as required. For instance, such items as premiums paid might be reported for various time periods--weekly, monthly, or annually. All premium values were converted to a standard time period before imputation.
- Selection of donors--The general process to select donors was the same for all groups. The process is a type of hot-deck imputation developed by Stiller and Dalzell (1997), described below.
- Creation of required values--Once a donor was selected, a value was created for the recipient case. Sometimes this was as simple as using the donor's item response and placing it in the recipient slot. In other cases, donor information was combined with information from the recipient in more complex ways to create the final value. Values also were edited against other recipient data to create a consistent set of responses.
Return To Top
A hot-deck method was used to select donor cases to provide information for recipients with items missing. This is a general class of methods by which donors and recipients are divided into prediction classes based on characteristics that predict the value of a given item. For each recipient with a missing data item, a donor in the same class for that variable is selected to provide information for the missing item. For instance, suppose that one needed to produce values of a plan's total premium when the employer did not respond. If the plan's premium were predicted by the type of provider and the State in which the plan was issued, then each time information on a plan's premium was missing, one could randomly select a plan with the same provider type and State and assign that selected plan's premium to the plan with a missing value. The method is based on the assumption, expressed in Kalton and Kasprzyk (1986), that the value of the missing response can be approximated by a regression model based on n parameters with an error 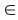 , with , with ![E[E] = 0](eeqp3.jpg) . Thus if y is the missing value, y can be written as: . Thus if y is the missing value, y can be written as:
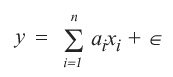
According to the model, the item being used from the donor has the same expected value as the recipient item being imputed. For the example above, two parameters--State and type of provider--predict y, the respondent's premium. All plans in the same cell determined by type of provider and State have the same expected premium.
A problem arises when there are no donors in a cell with a recipient. In this case, one needs to determine the best cell from which to select a donor. Many times, in practice, the person performing the imputation simply collapses two or more cells that have similar expected values of the variable to be imputed. The researcher in this case is using predictive mean matching (Little, 1988). This is a method for selecting a value for a recipient from another donor cell with the same or very similar expected value. Of all cells, the donor cell selected has an expected value of the item to be imputed that is the closest to the missing value for the recipient. In terms of expected values, the chosen cell would be termed the "nearest neighbor," among all cells that contain actual donors, to the cell in which the recipient lies. For the premium example above, if there is no plan with the same provider type and State as the recipient, then the default might be to find a donor in a neighboring State with the same type of providers.
The general method of selecting donors to provide information for imputation in the MEPS IC is similar to that described in Little (1988). Developed by Stiller and Dalzell (1997), it is a simple automated method to find a very close neighbor to the case with missing data. The method has the following steps:
Return To Top
- Determine the variables to use to define cells for a hot-deck process for a particular item.
- Rank the variables from least important to most important.
- If collapsing must occur, determine the point (going up the list of variables from least important to most important) at which collapsing is no longer acceptable.
- Divide the variables into two groups. Class variables are those that cannot be collapsed. Sort variables can be collapsed.
- Break the file of all respondents that are either donors or recipients for the item to be imputed into separate files determined by the class variables. Recipients within these subsets can receive data only from donors within the same subset. Thus, donors and recipients always have the same values for the class variables.
- Using the sort variables, sort each file defined by the cross of class variables so that the most important variables come first. A recipient's donor generally will be the first donor on the file above it in the sort order. Because the file is sorted from most important to least important, that donor will usually have all sort variables in common. If not, the values that do not match will be the least important variables.
Except for restrictions applied to keep from using the same donor too many times and cases in which there are multiple recipients in a row on the file, the donor selected is the nearest donor on the file to the recipient. (For more detail, see Stiller and Dalzell, 1997.)
Again using the example of missing premium information, suppose it were decided that type of plan was the most important variable and that a plan from a different State would be an acceptable donor if it had the same provider type. Provider type would be a class variable and State would be the sort variable. A separate file of cases with each different provider type would be produced. One would then process through each file individually, continuously updating the values of the current or nearest donor available in that portion of the file. When a case needing imputation arises, the donor currently available at that point is selected. If there is a large ratio of donors to recipients, as is generally the case, most recipients will be sorted together with donors that match on all or most variables. Because of the sort from most to least important, if the donor and recipient do not match completely, then the matching fails (collapsing occurs) on the least important variables first. The donor currently available will be the best or near-best match in the set.
Return To Top
This section of the report covers each of the groups of variables that were imputed for the MEPS IC. For each group, the variables to be imputed are shown with their questionnaire number. (The questionnaire is given in Appendix A.) Any needed preprocessing is described, sort variables used in the selection of all donors for the individual variables within the group are given, class variables used for imputation are described, and the step-by-step process used to create values for the recipient from the donor information is given. All logical edits are assumed to have been performed before the imputation takes place. Thus, for instance, if a respondent gave the total number of part-time employees in question D1b as zero and did not fill in how many were eligible or enrolled, these values were automatically set to zero. Because of this assumption, logical edits in process descriptions are not discussed.
Throughout the process, standard definitions of a responding establishment and responding plan are assumed. An establishment was considered a respondent if it answered either that it did or that it did not provide insurance for its employees and, if the establishment did provide insurance for some of its employees, it provided information on at least one of its plans. Responding plans are defined as those for which information was provided on at least one of the following items for the specific plan:
- Type of providers, question B2.
- Gatekeeper required, question B3.
- Purchased or self-insured, question B4.
- Plan enrollment, question B10b.
- Premiums and employer and employee contributions, question B11.
Return To Top
First Group of Variables
The questions in the first group are shown below, along with the applicable questionnaire number (Appendix A).
| D1a |
|
Total employees, total eligible, total enrolled. |
| D1b |
|
Total part-time employees, total part-time eligible, total part-time enrolled. |
| D1d |
|
Are retirees offered insurance? |
| D1d |
|
If retirees are offered insurance, which groups are eligible? |
Sort Variables
The sort variables are shown in Appendix B. In the order in which they are used, they are: age of firm, industry division group, industry division, Firm Size Class I, and establishment size.
Class Variables
Since this imputation applies only to establishments that offer health insurance, the donor set is immediately limited to the subset of respondents that offer health insurance. Another variable, Firm Size Class 2, is also used as a class variable to subset the population for imputation of this group of variables. This variable divides the firms that own the establishments into two groups based on the total employment of the firm (Appendix B). Using a firm size variable as a sort-order variable and a second firm size variable with fewer categories as a class variable allows the selection of a similar firm size class as a "nearest neighbor." However, the selection can only be made in the range of firm size classes defined by the variable Firm Size Class 2 (see Appendix B). Using two related variables in this way permits some use of other values of a given variable for the donor but sets a limit on those values by using a class variable with similar characteristics. This is done often in the MEPS IC imputation process. Industry is also often used as a sort variable and certain groups of industries as a class variable. This means that a donor can have a different industry from the recipient but must belong to the same larger industry group.
Return To Top Process
If necessary, the total number of employees was taken from the Standard Statistical Establishment List produced by the Census Bureau. This file, which contains a list of almost all private-sector business establishments within the United States, is used as the sampling frame for most Census establishment surveys. It is compiled each year and gives the total employment for the establishment as of the second week in March.
Once the total employment is available, the remaining variables in question D1a are imputed in order, using a separate imputation run for each. To impute total eligible employees, a donor for each recipient is selected from the set of all donors for this group (which is the set of respondents that completed all questions in the group). Two ratios are calculated from the donor: eligible employees to total employees and eligible employees to enrolled employees. If the recipient has reported the total enrolled, the eligible-to-enrolled ratio from the donor is applied to obtain the total eligible. In most cases, when the recipient has not reported the total enrolled, the eligible-to-total ratio is applied to the recipient value of total employment to obtain an estimate of the total eligible. The value of the total enrolled is then imputed by selecting a donor, calculating the ratio of the donor's total enrolled to total eligible, and applying this ratio to the recipient's total enrolled eligible employees.
Imputation is continued with the information on part-time employees, D1b. This is calculated by selecting another donor, calculating the ratio of the donor's part-time to total employees, and applying this ratio to the recipient's value of total employees. Total eligible and enrolled part-time employees are calculated using a process parallel to that used to calculate total eligible and enrolled employees: that is, ratios from the donors are applied sequentially, starting with the value of total part-time employees.
Because of the need for consistency in the data, there are minor differences in the process of imputing eligible and enrolled part-time employees and the process of imputing the total number of eligible and enrolled employees. Given that total values have been produced, these values create limits on the sets of values that part-time results can be.
Return To Top
- The two values, eligible and enrolled part-time employees, are both automatically set to zero if the number of part-time employees is imputed as zero.
- The donor set for eligible part-time employees is further limited to only those donors that reported having part-time employees.
- The donor set for enrolled part-time employees is limited to those donors that have eligible part-time employees.
- Each value for part-time employees is limited. These values cannot be set to a value greater than the similar value for all employees (question D1a). For instance, the value of enrolled part-time employees for a recipient is bounded by the value of the total number enrolled, which is imputed earlier in the process. Thus, to impute the number of enrolled part-time employees, one selects a donor and multiplies the recipient's number of part-time eligible employees times the donor's ratio of part-time enrolled employees to eligible part-time employees. This result is then checked against the recipient's total number of enrolled employees. If the imputed number of part-time employees enrolled is greater than the total, then the number of part-time enrolled is decreased to the same value as the total number enrolled.
The final imputation for this group of questions relates to the provision of health insurance to retirees, D1d. This is a two-part question that requires confirmation that the establishment offers health insurance to retirees before the second part of the question is completed. Both parts of the question are imputed in a similar manner. First, from the set of donors using the standard sort and class variables, a donor is selected to provide a yes/no response to all recipients that require an answer to whether insurance is offered to retirees. Second, for all recipients that answered yes to the first part of the question, including those that had a value of yes imputed for the first part of the question, an answer is imputed to tell what groups of retirees are offered health insurance, under 65 years and/or 65 years and over. Donors for this last step are limited to donors for the group that offers health insurance to retirees.
Return To Top
Second Group of Variables
The question in the second group deals with type of providers (questionnaire number B2 in Appendix A).
Sort Variables
The sort variables, shown in Appendix B, are Census Division, Firm Size Class 1, industry division group, industry division, and State.
Class Variables
The class variables are whether there is a deductible (part of question B14) and Firm Size Class 2.
Process
The process is simple and direct. The donor set is all plans with a response to question B2 (type of provider). Recipients are all responding plans with a missing value of B2. The value for the recipient is determined by direct substitution of the donor value.
Second Group of Variables for Nonresponding Plans
Sort Variables. The sort variables are Census Division, Firm Size Class 2, Firm Size Class 1, industry division group, industry division, and State.
Class Variable.The class variable is the number of plans for which information is requested.
Process. For the standard second group imputation, the value of type of providers, question B2, was imputed for responding plans. However, type of providers, B2, also can be imputed for nonresponding plans. This imputation is at the establishment level rather than the plan level. When establishments reported for some but not all the plans for which they were required to provide information, this imputation provides an answer to question B2 for the missing plans.
The donor set is the set of all establishments that reported for all the plans required by the survey. An establishment from this group was selected for each recipient establishment that was missing at least one plan. (Note that many establishments reported on some, but not all, plans. Thus an establishment could have reported B2 values for some plans and imputed values for other plans.) A recipient and donor both had to have reported the same number of plans (edited results of question A1).
The plans for both donor and recipient were sorted in this order: question B2 equal to 2, then B2 equal to 3, then B2 equal to 1, then any missing plans. This sets a one-to-one correspondence between the required donor and recipient plans. The plans from the recipient establishment without a value of question B2 were assigned the value of the corresponding donor plan.
Return To Top
Third Group of Variables
The questions in the third group are shown below, along with the applicable questionnaire number (Appendix A).
| B3 |
|
Does plan require referral to a specialist? |
| B9 |
|
Beginning of plan year. |
Sort Variables
The sort variables, shown in Appendix B, are Census Division, State, and Firm Size Class 2.
Class Variable
The class variable is type of providers (Question B2).
Process
Donors are all plans collected with the two questions (B3 and B9) completed. Recipients are all responding plans missing at least one of the two questions in the group. There is a separate donor selection for each question. Thus, a recipient missing both answers would likely have results from two different donors.
Note that, for this group, both donors and recipients are plans rather than establishments. This is a result of the questionnaire design. The questions in Section B of the questionnaire must be answered for every plan offered by an establishment, so answers and the imputation of these results are normally at the plan level. Questions in other sections are answered once for each establishment and thus are worked with at an establishment level.
Return To Top
Fourth Group of Variables
The questions in the fourth group are shown below, along with the applicable questionnaire number (Appendix A).
| B11a |
|
Total single premium only. |
| B11b |
|
Does employer offer family coverage? |
| B11b |
|
Total family premium only. |
Sort VariablesThe sort variables, shown in Appendix B, are Census Division, State, Firm Size Class 1, and industry division group. In addition, industry division is used for imputation of total single premium and whether employer offers family coverage, and total single premium is used for total family premium imputation only. Class VariablesThe class variables are provider type and Firm Size Class 2.
Process
Return To Top
Fifth Group of Variables
The question in the fifth group is shown below, along with the applicable questionnaire number (Appendix A). B4 Is the plan self-insured?
Sort Variables
The sort variables, shown in Appendix B, are industry division group, industry division, Firm Size Class 1, State, same firm.
Class Variables
The class variables are Firm Size Class 2 and "not all HMOs."
Process
To impute this variable requires the imputation of two variables, one at the establishment level and one at the plan level. A variable is created for each establishment that indicates if there are any self-insured plans at the establishment level. The class variable used for this imputation is whether the establishment offers a plan that is not an exclusive provider type plan. This is done because HMOs have been found to be much less likely to be self-insured. The donor set for this variable is the set of all establishments that provided an answer to question B4 (indemnification type) for all their plans. The recipients are those establishments for which the self-insured status cannot be determined. These are respondents that did not report in question B4 that at least one of their plans is self-insured and did not answer question B4 for all their plans.
Once it is established whether an establishment offers at least one self-insured plan, plans for establishments are logically edited. If establishments have a self-insured plan and only one plan, the plan is automatically self-insured. If establishments have no self-insured plans, all plans are assumed to be purchased plans.
For the remaining plans, information on self-insured status is imputed from establishments that have at least one self-insured plan. The donor set is the set of plans from establishments that have at least one self-insured plan. In order to perform this imputation, another class variable is added to the process. This is the provider type for the plan, the answer to question B3. Plans with different answers to question B3 have significant differences in the probability of being self-insured.
Return To Top
Sixth Group of Variables
The questions in the sixth group are shown below, along with the applicable questionnaire number (Appendix A).
B11a Employer and employee contributions for single coverage.
B11b Employer and employee contributions for family coverage.
Sort Variables
The sort variables, shown in Appendix B, are industry division group, industry division, Firm Size Class 1, Census Division, and State.
Class Variables
The class variables are Firm Size Class 2 and provider type.
Process
Employer and employee contributions were imputed at the firm level and industry division level. This means that employee contributions in any establishment within the same firm level within the same type of business were assumed to be highly correlated. To accomplish the imputation, first the average employee premium contributions for family and single coverage across all reporting establishments within the same industry division within the same firm level were calculated. For example, if Apex Corporation had both a manufacturing and retailing subsidiary, they were treated separately. If an establishment within the same firm and industry division failed to report this information and other establishments within the same firm and industry division reported, the average employee contribution percentage for the former was assumed to be the same as for the latter. Thus, for Apex, if a manufacturing establishment was missing employee contributions, this information was imputed, if possible, using the average of other Apex manufacturing establishments.
For firm/industry division combinations that did report for some establishments and could not be completed in this fashion, a donor firm/industry division combination was selected using the standard hot-deck procedure, using the sort and class variables described earlier. In this process, the State for a multi-State firm was set equal to missing.
The donor's average employee single and family contribution percentages were applied to the single and family total premiums for all recipient plans to produce the employee contributions for the recipient plans. Once these were calculated, employer contributions were obtained by subtraction from the appropriate total premium.
Return To Top
Seventh Group of Variables
The question in the seventh group is shown below, along with the applicable questionnaire number (Appendix A).
B10b Total active employees enrolled in an individual plan.
Sort Variables
The sort variables, shown in Appendix B, are industry division group, industry division, Firm Size Class 1, and State.
Class Variables
The class variables are plan count (number of plans offered to employees) and Firm Size Class 2.
Process
Imputation for this question was limited to establishments that had two or more plans and failed to report for at least two of the plans for which information was requested. All other plans with missing data on total active employees enrolled in a plan can be assigned a value equal to the total enrollment for the establishment, question D1a, less the values for question B10b for the remaining reported plans.
Donors for the process were establishments that offered employees at least two health plans and responded to this question for all required plans. To start the process, donors and recipients were assigned a value called plan count. This was the number of plans the respondent indicated it provided to employees. Plan count was always greater than one for this set.
Selection of donors for recipients was done using the standard method with the sort and class variables given. This means that donors and recipients had the same value of plan count.
Each plan within a selected donor establishment was assigned the proportion of the establishment's total active enrollment that the plan represented (question D1a). If a private establishment offered more than four plans, it was asked to report for the three largest plans plus a fourth selected at random from the remaining plans.
The plans within each donor and recipient establishment were sorted by the values for reported active enrollees. Proportions were assigned from donor to recipient by the sort order.
If the recipient failed to report the active enrollment for all plans, then enrollment for each of the recipient's plans was calculated as the imputed proportion of the establishment's active enrollment. If the recipient reported for some but not all plans, the remaining enrollment in the recipient establishment was distributed among the unreported recipient plans using the relative sizes of the proportions assigned from the donor. For example, suppose there were three plans in an establishment with a total active enrollment of 200 and the respondent gave the active enrollment for the first plan as 100. Further, suppose the donor's three plans represented 50, 30, and 20 percent of the donor's total active enrollment. The remaining 100 active enrollment would be distributed in a ratio of 3 to 2, based on the relative relationship between the two smallest donor plans.
This method attempted to create a distribution of enrollees for the recipient establishment's plans that was similar to that of another establishment. This was done by considering all the plans from both donors and recipients, each with an equal number of plans, in a single step.
Return To Top
In the imputation process for sampled governments, the same data items are imputed as for the private-sector establishments. The process is similar to that for the private sector. The only differences are the sort and class variables used. For government case imputation, the same sort variables are used for all data groups. These are, in sort order, Census Division, State, and government employment size. No class variables are used to describe the government. The only class variables used are the specialized variables for plans that apply to a particular imputation group. For instance, for Group 4 in the private sector, Firm Size Class 2 and provider type are class variables. For Group 4 government case imputation, Firm Size Class 2 is dropped but provider type is kept. This is because size would refer to government and is not used, but provider type is a characteristic of the plan and these variables are used.
Return To Top
Review of the results of the imputation and its effects on estimates made with these critical data items was very thorough. After the data were imputed, results were edited to determine if the process had produced inconsistencies in the data. Cell averages were examined before and after imputation to determine if key factors had been missed. During the actual process, problems were found and corrected in this way.
After internal review of the results, estimates were made and benchmarked to outside sources. One key part of this process involved checks against results of the 1994 National Employer Health Insurance Survey (NEHIS), conducted by the National Center for Health Statistics (NCHS). NEHIS was a one-time survey whose purpose, sample design, and questionnaire were similar to those of the MEPS IC (National Center for Health Statistics, 1997). There were some differences in total employment and numbers of establishments, which were easily explained by the number of years between the two surveys and slight differences in the survey frames used. However, the relative numbers benchmarked quite well and had few significant statistical differences. For instance, the estimate of the percent of private-sector establishments that offered health insurance was 52.8 percent for the MEPS IC and 51.6 percent for the NEHIS. Likewise, the percent of workers eligible for health insurance was 80.9 percent in the MEPS IC and 81.7 percent for the NEHIS. A more thorough review of the comparison of the two surveys and some individual numbers from other sources can be found in the review written by Thorpe and Florence (1999).
Return To Top
Cohen SB. Sample design of the 1996 Medical Expenditure Panel Survey Household Component. Rockville (MD): Agency for Health Care Policy and Research; 1997. MEPS Methodology Report No. 2. AHCPR Pub. No. 97-0027.
Cox BG, Cohen SB. Methodological issues for health care surveys. New York: Marcel Dekker; 1985.
Kalton G, Kasprzyk D. The treatment of missing survey data. Survey Methodology 1986;12(1):1-16.
Little RJA. Missing data adjustments in large surveys. Journal of Business and Economic Statistics 1988;6(3):287-96.
National Center for Health Statistics: Employer-sponsored health insurance: State and national estimates. Hyattsville (MD); 1997. DHHS Pub. No. (PHS) 98-1017.
Sommers JP. List sample design of the 1996 Medical Expenditure Panel Survey Insurance Component. Rockville, MD: Agency for Health Care Policy and Research; 1999. MEPS Methodology Report No. 6. AHCPR Pub. No. 99-0037.
Stiller J, Dalzell D. Hot-deck imputation with SAS arrays and macros for large surveys. Proceedings of the 10th Annual NESUG Conference; 1997. North East SAS Users Group. p. 709-14.
Thorpe K, Florence C. An examination of the Medical Expenditure Panel Survey Insurance Component [unpublished report]. Rockville (MD): Agency for Health Care Policy and Research; 1999.
Return To Top

Return To Top

Return To Top

Return To Top

Return To Top

Return To Top

Return To Top
Appendix B. Definitions of Selected Variables
Firm Size Class 1
| 1 if firm employment = |
0-5 |
| 2 if firm employment = |
6-24 |
| 3 if firm employment = |
25-99 |
| 4 if firm employment = |
100-999 |
| 5 if firm employment = |
1,000 or more |
Firm Size Class 2
| 1 if firm employment = |
0-249 |
| 2 if firm employment = |
250 or more |
Establishment size
| 1 if establishment employment = |
0-10 |
| 2 if establishment employment = |
11 or more |
Return To Top
Industry division (Standard Industry Code--SIC)
Agriculture if two-digit SIC = 01-09
Construction if two-digit SIC = 15-17
Retail trade if two-digit SIC = 52-59
Mining if two-digit SIC = 10-14
Finance, insurance, and real estate if two-digit SIC = 60-67
Wholesale trade if two-digit SIC = 50-51
Manufacturing if two-digit SIC = 20-39
Transportation, communication, and utilities if two-digit SIC = 40-49
Services if two-digit SIC = 70-89
Industry division group
1 if industry division = agriculture, construction, or retail trade
2 if industry division = manufacturing, transportation, communication, utilities, or services
3 if industry division = mining, finance, insurance, real estate, or wholesale trade
Firm age
| 1 if age = |
0-16 years |
| 2 if age = |
17 years or more |
Census Division
New England if State = ME, NH, VT, MA, CT, RI
Mid-Atlantic if State = NY, NJ, PA
East North Central if State = OH, IN, IL, MI, WI
West North Central if State = MN, IA, MO, ND, SD, NE, KS
South Atlantic if State = DE, MD, DC, VA, WV, NC, SC, GA, FL
East South Central if State = KY, TN, AL, MS
West South Central if State = AR, LA, OK, TX
Mountain if State = MT, ID, WY, CO, NM, AZ, UT, NV
Pacific if State = WA, OR, CA, AK, HI
Return To Top
Suggested Citation:
Methodology Report #10: Imputation of Employer Information for the 1996 MEPS Insurance Component. June 2000. Agency for Healthcare Research and Quality, Rockville, MD. http://www.meps.ahrq.gov/data_files/publications/mr10/mr10.shtml
|
|
